Стационарность

Если все свойства случайного процесса (плотности распределения вероятностей) не зависят от времени, случайный процесс называется стационарным (в узком смысле). Иначе процесс – нестационарный, его свойства со временем изменяются. Строго говоря, все реальные процессы – нестационарные, они когда-то начались и когда-то закончатся. Однако часто на практике можно считать, что на интересующем нас интервале времени (например, во время перехода судна из одного порта в другой) свойства случайных процессов (волнения, ветра) не изменяются. Это допущение позволяет существенно упростить решение многих задач.

Стационарность – это очень сильное допущение. Чтобы доказать его справедливость, нужно знать все плотности распределения[3] в любой момент времени, а они чаще всего неизвестны. К счастью, стационарность (в узком смысле) совсем не требуется в инженерных задачах. Вместо этого достаточно рассматривать процессы, стационарные в широком смысле, для которых

1) математическое ожидание не зависит от времени;

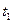2) корреляционная функция зависит только только от того, насколько моменты и 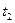далеки друг от друга, то есть от разности , поэтому ее часто записывают в виде , где .

Далее, говоря о стационарных процессах, мы будем иметь в виду процессы, стационарные в широком смысле.