Что такое случайный процесс?

Случайный процесс – это случайная функция времени. Это означает, что наблюдатель «видит» только одну реализацию случайного процесса (она выделена на рисунке красным цветом) из множества возможных функций (синие линии).

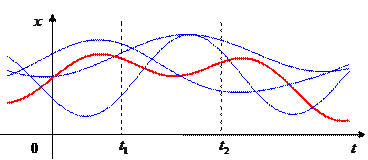
Полный набор всех возможных реализаций называют ансамблем. Случайный процесс – это и есть ансамбль реализаций, а не функция в обычном понимании. Далее будем обозначать весь ансамбль (случайный процесс) через 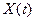, а отдельную реализацию – через .

Характеристикой случайного процесса (точнее – характеристикой ансамбля реализаций) в каждый фиксированный момент времени 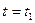является плотность распределения вероятности 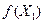случайной величины 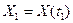. По этим данным можно найти среднее значение (математическое ожидание), дисперсию, СКВО и другие характеристики случайного процесса. Процессы с нулевым средним значением называются центрированными.

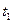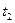Для многих (хотя и не для всех) случайных процессов значения в моменты времени и как-то связаны. Чтобы оценить связь случайных величин 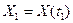и 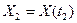используют корреляцию – математическое ожидание произведения :

.

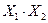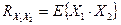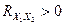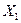Корреляция позволяет выявить линейную зависимость между двумя величинами. В случае знаки и 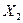чаще всего совпадают (оба положительные или оба отрицательные), а при 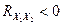– больше вероятность того, что знаки разные. Если 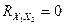, величины 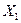и 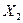называются некоррелированными. Важно понимать, что это не означает, что они независимы. С другой стороны, независимые величины всегда некоррелированы. Для случайных величин с нормальным распределением некоррелированность одновременно означает и независимость.

Вспоминая, что 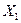и 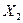– это значения случайного процесса в моменты 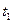и 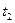, можно рассматривать корреляцию как функцию двух аргументов:

.

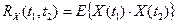Эта функция называется корреляционной (или автокорреляционной) функцией случайного процесса 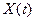. В этой формуле используется усреднение по ансамблю, то есть по всем возможным реализациям случайного процесса. Практически эта операция трудновыполнима, так как нужно иметь полную информацию о процессе (распределения вероятностей).

Если случайный процесс – это напряжение в вольтах, то его корреляционная функция измеряется в В², так же, как средний квадрат и дисперсия.