Тема 3. Дифференциальное исчисление функций одной переменной. 1. Привести примеры функций, недифференцируемых на бесконечном ограниченном множестве.

1. Привести примеры функций, недифференцируемых на бесконечном ограниченном множестве.

2. Функция в данной точке дифференцируема. Следует ли отсюда, что она непрерывна в этой точке?

3. Сформулируйте общие правила дифференцирования функций.

4. Найти формулы Маклорена произвольного порядка для функции .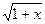

5. В чем заключается правило Лопиталя?

6. Как найти максимумы и минимумы функции?

7. Приведите пример, показывающий, что обращение производной в нуль не является достаточным условием экстремума функции.

8. Решить примеры из сборника 8.в.1 по теме 3.

Тема 4. Дифференциальное исчисление функций нескольких переменных.

1. Привести пример функции двух переменных непрерывной, но не имеющей частных производных в нуле.

2. Изучить метод множителей Лагранжа.

3. Решить примеры из сборника 8.в.1 по теме 3.

Тема 5. Неопределенный интеграл.

1. Доказать формулу интегрирования по частям для неопределенного интеграла.

2. Доказать теорему единственности неопределенного интеграла.

3. Вывести таблицу неопределенных интегралов.

4. Решить примеры из сборника 8.в.1 по теме 4.

Тема 6. Определенный интеграл.

1. Найти точное значение интеграла .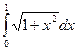

2. Найти приближенное значение 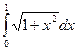по формуле трапеций с .

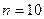3. Доказать теорему о среднем для определенного интеграла от непрерывной функции.

4. Доказать теорему о дифференцировании определенного интеграла от непрерывной функции по верхнему пределу.

5. Решить примеры из сборника 8.в.1 по теме 6.

Тема 7. Дифференциальные уравнения.

1. Геометрический смысл общего и частного решений дифференциального уравнения.

2. Какое дифференциальное уравнение первого порядка называется линейным и как оно интегрируется?

3. Какое дифференциальное уравнение второго порядка называется линейным? В каких случаях оно называется однородным, а в каких неоднородным?

4. Решить примеры из сборника 8.в.1 по теме 7.