Оценочные средства для промежуточной аттестации.
Вопросы для подготовки к экзамену.
Теоретические вопросы для подготовки к промежуточной аттестации за 1-ый семестр.
1. Понятие функции. Способы задания функций. Примеры. Элементарные функции.
2. Числовая последовательность. Предел числовой последовательности. Примеры.
3. Предел функции (два определения). Основные теоремы о пределах. Второй замечательный предел.
4. Бесконечно малые и бесконечно большие функции. Первый замечательный предел, его геометрический смысл.
5. Предел функции. Непрерывность функции в точке. Точки разрыва функции и их классификация. Примеры.
6. Функции, непрерывные на отрезке (определение). Свойства функций, непрерывных на отрезке.
7. Производная функции, её геометрический и физический смысл. Дифференцируемость и непрерывность функции.
8. Производные элементарных функций.
9. Основные правила дифференцирования.
10. Дифференциал функции и его использование в приближенных вычислениях. Производные и дифференциалы высших порядков.
11. Правило Лопиталя.
12. Возрастание и убывание функции. Исследование возрастания и убывания функции с помощью производной.
13. Экстремум функции. Необходимое условие экстремума. Достаточные условия экстремума.
14. Формулы Тейлора и Маклорена.
15. Выпуклость графика функции. Исследование выпуклости с помощью второй производной. Точки перегиба.
16. Асимптоты. Общая схема исследования функций.
17. Понятие функции нескольких переменных, предел и непрерывность, частные производные и дифференциал.
18. Производная функции двух переменных по направлению. Градиент и его свойства.
19. Необходимое и достаточное условия локального экстремума функции двух переменных.
20. Условный экстремум.
21. Первообразная. Понятие неопределенного интеграла.
22. Свойства неопределенного интеграла. Табличные интегралы.
23. Замена переменной в неопределенном интеграле. Формула интегрирования по частям.
24 Определенный интеграл, его геометрический смысл и свойства. Формула Ньютона - Лейбница.
25. Замена переменной в определенном интеграле и интегрирование по частям.
26. Геометрические приложения определенного интеграла.
27. Несобственные интегралы. Определение, примеры.
28. Понятие о дифференциальном уравнении. Общее и частное решения. Дифференциальное уравнение первого порядка. Задача Коши. Теорема о существовании и единственности решения.
29. Дифференциальные уравнения первого порядка с разделяющимися переменными.
30. Линейные дифференциальные уравнения первого порядка и методы их решения.
31. Линейные дифференциальные уравнения второго порядка. Теоремы об общих решениях однородного и неоднородного уравнений.
32. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение. Общее решение для различных случаев.
33. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
.
Теоретические вопросы для подготовки к промежуточной аттестации за 2-ой семестр.
1. Системы линейных уравнений , основные понятия. Метод Гаусса.
2. Ранг матрицы. Теорема Кронекера – Капелли. Решение неопределенных систем линейных уравнений. Общее, частное и базисное решения системы линейных уравнений.
3. Определители 2-го и 3-го порядка и их свойства.
4. Определители n-го порядка и их свойства.
5. Матрицы и действия с ними. Свойства операций над матрицами.
6. Обратная матрица и способы ее нахождения.
7. Решение систем линейных уравнений с помощью формул Крамера и с помощью обратной матрицы.
8. Векторы и линейные операции над ними. Арифметическое n – мерное векторное пространство Rn..Геометрический смысл пространств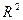 
и 
.
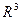9. Скалярное произведение векторов и его свойства. Длина вектора, угол между векторами.
10. Линейно зависимые и линейно независимые системы векторов.
11. Базис пространства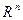 
. Разложение вектора по произвольному базису.
12. Различные виды уравнений прямой на плоскости. Угол между двумя прямыми.
13. Прямая и плоскость в пространстве.
14. Основные понятия теории вероятностей. Операции над событиями.
15. Аксиоматическое построение теории вероятностей. Классическая вероятностная схема.
16. Элементы комбинаторики и вычисление вероятности событий. Геометрическая вероятность.
17. Теоремы сложения и умножения вероятностей.
18. Условная вероятность. Независимость событий. Теорема умножения вероятностей.
19. Формула полной вероятности.
20. Формула Бейеса.
21. Вероятность событий в схеме Бернулли.
22. Локальная и интегральная теоремы Муавра – Лапласа.
23. Определение случайной величины. Функция распределения и ее свойства.
24. Закон распределения, полигон и функция распределения дискретной случайной величины.
25. Плотность распределения и функция распределения непрерывной случайной величины.
26. Математическое ожидание дискретной и непрерывной случайной величины.
27. Дисперсия и среднее квадратическое отклонение дискретной и непрерывной случайной величины.
28. Распределения дискретных случайных величин: биномиальное, Пуассона. Их числовые характеристики.
29. Равномерное и показательное распределения, их числовые характеристики.
30. Нормальное распределение и его числовые характеристики
Билеты (варианты тестов) к зачетам (и экзаменам) состоят из нескольких теоретических вопросов, выбранных из приведенных выше списков, и задач, аналогичных решаемым на cеминарах.
Программа составлена в соответствии с требованиями ФГОС ВПО по направлению 080200 - менеджмент.
Коды сформированных компетенций: ОК-2, ОК-5, ОК-6, ОК-15.
Разработчики:
Дата добавления: 2014-12-07; просмотров: 748;