V. ОЦЕНОЧНЫЕ СРЕДСТВА
Курсовая работа по дисциплине «Эконометрика» не предусмотрена.
Примерные варианты письменных домашних заданий
Один из вариантов письменного домашнего задания №1.
Задача. Проводится анализ взаимосвязи количества населения Х (млн. чел.) и количества практикующих врачей Y (тыс. чел.) за десятилетний период:
| год | ||||||||||
| Х | 10.0 | 10.3 | 10.4 | 10.55 | 10.6 | 10.7 | 10.75 | 10.9 | 10.9 | 11.0 |
| Y | 12.1 | 12.6 | 13.0 | 13.8 | 14.9 | 16.0 | 18.0 | 20.0 | 21.0 | 22.0 |
Задание.
1. Постройте корреляционное поле и по его виду определите форму зависимости между Х и Y.
- Оцените по МНК параметры уравнения линейной регрессии.
- Оцените выборочный коэффициент корреляции и сделайте предварительный вывод о силе линейной взаимосвязи параметров Х и Y.
- Проверьте качество уравнения регрессии:
- значимость параметров регрессии;
- интервальные оценки параметров регрессии;
- значимость уравнения регрессии в целом;
- интервальную оценку остаточной дисперсии.
- Проинтерпретируйте результаты.
- Сделайте прогноз среднего (индивидуального) значения количества практикующих врачей и постройте доверительный интервал для него при значении Х = Хпрогн..
Уровень значимости 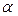 = 0,05; Хпрогн= 11.5 (млн. чел.).
= 0,05; Хпрогн= 11.5 (млн. чел.).
Один из вариантов письменного домашнего задания №2.
Задача . Изучается влияние выработки продукции на одного работника (х1 - единиц) и доли продукции, производимой на экспорт (х2 - %) на величину прибыли (у - млн руб.) концерна. Для этого по 10 предприятиям концерна были получены данные приведенные в таблице. Построить регрессионную модель: у = β0 + β 1 х1 + β 2 х2 + ε
| i | хi1 | хi2 | yi | i | хi1 | хi2 | yi |
Задание.
- По МНК оценить коэффициенты линейной регрессии βi , i =0, 1, 2 и записать выборочное уравнение регрессии.
- Оценить статистическую значимость найденных параметров регрессии b i , i =0, 1, 2.
- В соответствие с заданным значением
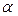 построить доверительные интервалы для найденных параметров;
построить доверительные интервалы для найденных параметров; - В соответствие с заданным значением
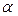 построить доверительный интервал для остаточной дисперсии;
построить доверительный интервал для остаточной дисперсии; - Вычислить коэффициент детерминации R2 и оценить его статистическую значимость при заданном значении
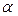 ;
; - Определить какой процент разброса зависимой переменной объясняется данной регрессией;
- Сравнить коэффициент детерминации R2 со скорректированным коэффициентом детерминации;
- Посредством коэффициентов b i , i = 1, 2, влияние объясняющих переменных Х1, Х2 на изменение объясняемой переменной;
- Спрогнозировать значение объясняемой переменной Yпрогн для прогнозных значений Х1 прогн , Х2 прогн и построить доверительный интервал для среднего (индивидуального) значения Yпрогн;
Х1 прогн = 14 единиц, Х2 прогн =8 %, 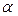 = 0,01.
= 0,01.
Один из вариантов письменного домашнего задания №3.
Задача . По этой теме используется задача, приведенная в письменном домашнем задании №1.
Задание.
1. По данным таблицы к линейной модели, полученной в письменном домашнем задании №1 : а) применить тест ранговой корреляции Спирмена для оценки гетероскедастичности при 5% уровне значимости; б) применить тест Голдфелда-Квандта для оценки гетероскедастичности при 5% уровне значимости.
2. По данным таблицы рассчитать: а) параметры степенной функции у=β0 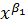 *ε; б) параметры равносторонней гиперболы у=β0+β1/x+ε; в) параметры экспоненциальной функции у=
*ε; б) параметры равносторонней гиперболы у=β0+β1/x+ε; в) параметры экспоненциальной функции у= 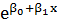 *ε; г) параметры полулогарифмической функции у=β0+β 1lnx+ε; д) параметры обратной функции у=1/(β0+β1x+ε); е) параметры функции у=β0+β1
*ε; г) параметры полулогарифмической функции у=β0+β 1lnx+ε; д) параметры обратной функции у=1/(β0+β1x+ε); е) параметры функции у=β0+β1 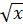 +ε; ж) параметры показательной функции у=β0
+ε; ж) параметры показательной функции у=β0 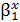 *ε; з) оценить с надежностью 0.95 значимость полученных уравнений с использованием F-критерия.
*ε; з) оценить с надежностью 0.95 значимость полученных уравнений с использованием F-критерия.
3. По данным таблицы для временного ряда хt: а) найти уравнение неслучайной составляющей (тренда), полагая тренд линейным; б) выявить на уровне значимости 0.05 наличие автокорреляции возмущений с использованием критерия Дарбина-Уотсона; в) найти с надежностью 0.95 интервальную оценку остаточной дисперсии 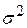 , полагая тренд линейным; г) найти коэффициент автокорреляции (для лага τ=1,2,3); д) найти с надежностью 0.95 интервальную оценку коэффициента регрессии β1, полагая тренд линейным; е) оценить с надежностью 0.95 значимость коэффициента парного регрессии с использованием t-критерия, полагая тренд линейным; ж) найти точечную и с надежностью 0.95 интервальную оценку прогноза среднего (индивидуального) значения количества населения на момент времени t=11 (одиннадцатый год), полагая тренд линейным; з) проверить с надежностью 0.95 значимость парной регрессии с использованием F-критерия, полагая тренд линейным.
, полагая тренд линейным; г) найти коэффициент автокорреляции (для лага τ=1,2,3); д) найти с надежностью 0.95 интервальную оценку коэффициента регрессии β1, полагая тренд линейным; е) оценить с надежностью 0.95 значимость коэффициента парного регрессии с использованием t-критерия, полагая тренд линейным; ж) найти точечную и с надежностью 0.95 интервальную оценку прогноза среднего (индивидуального) значения количества населения на момент времени t=11 (одиннадцатый год), полагая тренд линейным; з) проверить с надежностью 0.95 значимость парной регрессии с использованием F-критерия, полагая тренд линейным.
Вопросы для подготовки к защите индивидуального задания:
1. Что такое функция регрессии?
2. Назовите основные причины наличия в регрессионной модели случайного отклонения.
3. Что понимается под спецификацией модели, и как она осуществляется?
4. В чем состоит различие между теоретическим и эмпирическим уравнениями регрессии?
5. В чем суть метода наименьших квадратов (МНК)?
6. Приведите формулы расчета коэффициентов эмпирического парного линейного уравнения регрессии по МНК.
7. Как связаны эмпирические коэффициенты линейной регрессии с выборочным коэффициентом корреляции?
8. Проинтерпретируйте коэффициенты эмпирического парного линейного уравнения регрессии.
9. Как определяются стандартные ошибки регрессии и коэффициентов регрессии?
10. Опишите схему проверки гипотез о величине коэффициентов регрессии.
11. В чем суть статистической значимости коэффициентов регрессии?
12. Приведите схему определения интервальных оценок коэффициентов регрессии.
13. Как строится и что позволяет определить доверительный интервал для условного математического ожидания зависимой переменной?
14. В чем суть предсказания индивидуальных значений зависимой переменной?
15. Объясните суть коэффициента детерминации.
16. В каких пределах изменяется коэффициент детерминации?
Вопросы к экзамену
Пример экзаменационного билета в Приложении 2
1. В чем состоит различие между теоретическим и эмпирическим уравнениями регрессии?
2. В чем суть метода наименьших квадратов (МНК)?
3. Приведите формулы расчета коэффициентов эмпирического парного линейного уравнения регрессии по МНК.
4. Как определяются стандартные ошибки регрессии и коэффициентов регрессии?
5. Опишите схему проверки гипотез о величине коэффициентов регрессии.
6. В чем суть статистической значимости коэффициентов регрессии?
7. Приведите схему определения интервальных оценок коэффициентов регрессии.
8. Как строится и что позволяет определить доверительный интервал для условного математического ожидания зависимой переменной?
9. В чем суть предсказания индивидуальных значений зависимой переменной?
10. Объясните суть коэффициента детерминации.
11. Что представляет собой случайный член регрессионного уравнения? Приведите пример его экономической интерпретации.
12. Перечислите предпосылки классической модели линейной регрессии.
13. Что такое “несмещенная оценка коэффициента уравнения регрессии”?
14. Что такое “эффективная оценка коэффициента уравнения регрессии”?
15. Что такое “состоятельная оценка коэффициента уравнения регрессии”?
16. В чем суть метода наименьших квадратов для построения множественного линейного уравнения регрессии?
17. Приведите формулы расчета коэффициентов эмпирического линейного уравнения регрессии по МНК в матричной форме.
18. Как проверить статистическую значимость регрессионного уравнения?
19. Как проверить статистическую значимость коэффициента детерминации?
20. Чем скорректированный коэффициент детерминации отличается от обычного?
21. Как осуществляется анализ статистической значимости коэффициента детерминации?
22. Как используется F – статистика в регрессионном анализе?
23. В чем суть статистики Дарбина-Уотсона и как она связана с коэффициентом корреляции между соседними отклонениями?
24. Как анализируется статистическая значимость статистики Дарбина-Уотсона?
25. Приведите примеры нелинейных моделей, используемых в эконометрике.
26. Какие из известных вам типов нелинейных моделей поддаются непосредственной линеаризации?
27. Как линеаризуются модели гиперболического вида?
28. Как линеаризуются модели экспоненциального вида?
29. Как линеаризуются модели степенного вида?
30. Как линеаризуются модели логарифмического вида?
31. Каковы признаки качественной регрессионной модели?
32. Назовите основные виды ошибок спецификации.
33. Как можно обнаружить ошибки спецификации?
34. Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена?
35. В чем суть теста Рамсея?
36. Что такое гомоскедастичность и гетероскедастичность?
37. Приведите пример взаимоотношений в экономике, описываемых моделью с гетероскедастичными остатками.
38. Каким образом осуществляется проверка эконометрической модели на гомоскедастичность?
39. Почему нельзя применять классический МНК в случае гетероскедастичности?
40. Какие преобразования исходных данных нужно провести в случае обнаружения гетероскедастичности?
41. В чем суть метода взвешенных наименьших квадратов (ВМНК)?
42. Как вы понимаете термин «автокорреляция остатков»?
43. Приведите пример взаимоотношений в экономике, описываемых моделью с автокоррелированными остатками.
44. Каковы последствия применения классического МНК к модели с автокоррелированными остатками?
45. Каким образом осуществляется проверка эконометрической модели на автокорреляцию остатков?
46. Опишите схему использования статистики DW Дарбина-Уотсона.
47. Какие преобразования исходных данных нужно провести в случае обнаружения автокорреляции остатков?
48. Что такое мультиколлинеарность?
49. По каким проявлениям можно судить о наличии мультиколлинеарности в оцененной модели?
50. Каковы негативные последствия мультиколлинеарности?
51. Перечислите основные методы устранения мультиколлинеарности.
52. Перечислите основные элементы временного ряда.
53. Что такое автокорреляция уровней временного ряда и как ее можно оценить количественно?
54. Дайте определение автокорреляционной функции временного ряда.
55. Перечислите основные виды трендов.
56. Перечислите этапы построения аддитивной модели временного ряда.
57. В чем суть выравнивания уровней ряда методом скользящей средней?
58. Поясните смысл применения фиктивных переменных для моделирования сезонных колебаний.
59. В чем заключаются основные причины использования систем одновременных уравнений?
60. Каковы различия между структурными уравнениями системы и уравнениями в приведенной форме?
61. В чем суть КМНК?
Примеры вариантов письменных заданий на экзамене
Вариант 1.
В следующей выборке представлены данные по количеству Y и цене Х блага, приобретаемого домохозяйством ежемесячно в течение года:
| месяц | ||||||||||||
| Х | ||||||||||||
| Y |
По данным таблицы: а) применить тест ранговой корреляции Спирмэна для оценки гетероскедастичности линейного уравнения регрессии Y по Х при 5% уровне значимости. Известно, что: 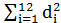 =253,5; б) рассчитать параметры степенной функции у=β0
=253,5; б) рассчитать параметры степенной функции у=β0 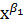 *ε. Известно, что:
*ε. Известно, что: 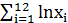 =39.8;
=39.8; 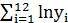 =48.8;
=48.8; 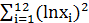 =134.5;
=134.5; 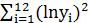 =200.3;
=200.3; 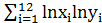 =160.0; в) для временного ряда yt оценить с надежностью 0.95 значимость коэффициента регрессии β1 с использованием t-критерия, полагая тренд линейным. Известно, что:
=160.0; в) для временного ряда yt оценить с надежностью 0.95 значимость коэффициента регрессии β1 с использованием t-критерия, полагая тренд линейным. Известно, что: 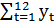 =760;
=760; 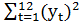 =55750;
=55750; 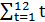 =78;
=78; 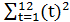 =650;
=650; 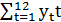 =4070.
=4070.
Вариант 2.
Имеются данные за 10 лет по прибылям Х и Y (в %) двух компаний:
| год | ||||||||||
| Х | 19.2 | 15.8 | 12.5 | 10.3 | 5.7 | 5.8 | 3.5 | 5.2 | 7.3 | 6.7 |
| Y | 20.1 | 18.0 | 10.3 | 12.5 | 6.0 | 6.8 | 2.8 | 3.0 | 8.5 | 8.0 |
По данным таблицы: а) применить тест Голдфельда-Квандта для оценки гетероскедастичности линейного уравнения регрессии Y по Х при 5% уровне значимости. Известно, что: 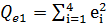 =4,5 и
=4,5 и 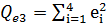 =12,8; б) рассчитать параметры степенной функции у=β0
=12,8; б) рассчитать параметры степенной функции у=β0 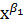 *ε. Известно, что:
*ε. Известно, что: 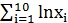 =20.9;
=20.9; 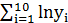 =20.8;
=20.8; 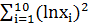 =46.1;
=46.1; 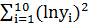 =47.2;
=47.2; 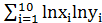 =46.4; в) для временного ряда yt оценить тесноту и направление связи между переменными Y и t с помощью коэффициента корреляции, полагая тренд линейным. Известно, что:
=46.4; в) для временного ряда yt оценить тесноту и направление связи между переменными Y и t с помощью коэффициента корреляции, полагая тренд линейным. Известно, что: 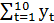 =96;
=96; 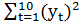 =1226;
=1226; 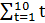 =55;
=55; 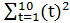 =385;
=385; 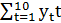 =407,9.
=407,9.
Вариант 3.
В следующей выборке представлены данные по количеству Y и цене Х блага, приобретаемого домохозяйством ежемесячно в течение года:
| месяц | ||||||||||||
| Х | ||||||||||||
| Y |
По данным таблицы: а) найти с надежностью 0.95 интервальную оценку коэффициента регрессии β1 и пояснить её смысл. Известно, что: 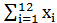 =360;
=360; 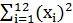 =12150;
=12150; 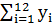 =760;
=760; 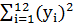 =55750;
=55750; 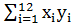 =19925; б) рассчитать параметры экспоненциальной функции у=
=19925; б) рассчитать параметры экспоненциальной функции у= 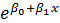 *ε. Известно, что:
*ε. Известно, что: 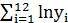 =48.8;
=48.8; 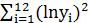 =200.3;
=200.3; 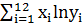 =1416; в) для временного ряда yt выявить на уровне значимости 0.05 наличие автокорреляции остатков с использованием критерия Дарбина-Уотсона. Известно, что:
=1416; в) для временного ряда yt выявить на уровне значимости 0.05 наличие автокорреляции остатков с использованием критерия Дарбина-Уотсона. Известно, что: 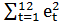 =2324;
=2324; 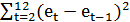 =5434.
=5434.
Вариант 4.
Имеются данные за 10 лет по прибылям Х и Y (в %) двух компаний:
| год | ||||||||||
| Х | 19.2 | 15.8 | 12.5 | 10.3 | 5.7 | 5.8 | 3.5 | 5.2 | 7.3 | 6.7 |
| Y | 20.1 | 18.0 | 10.3 | 12.5 | 6.0 | 6.8 | 2.8 | 3.0 | 8.5 | 8.0 |
По данным таблицы: а) найти 95%-ный доверительный интервал для индивидуального значения прибыли компании при прибыли другой компании равной 5% для линейного уравнения регрессии Y по Х и пояснить его смысл. Известно, что: 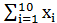 =92;
=92; 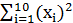 =1084.2;
=1084.2; 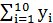 =96;
=96; 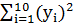 =1225.7;
=1225.7; 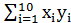 =1142.5; б) рассчитать параметры полулогарифмической функции у=β0+β1lnx+ε. Известно, что:
=1142.5; б) рассчитать параметры полулогарифмической функции у=β0+β1lnx+ε. Известно, что: 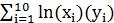 =227.2;
=227.2; 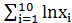 =20.8;
=20.8; 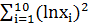 =46.1; в) для временного ряда yt проверить с надежностью 0.95 значимость парной регрессии с использованием F-критерия, полагая тренд линейным. Известно, что:
=46.1; в) для временного ряда yt проверить с надежностью 0.95 значимость парной регрессии с использованием F-критерия, полагая тренд линейным. Известно, что: 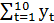 =96;
=96; 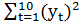 =1226;
=1226; 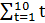 =55;
=55; 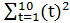 =385;
=385; 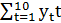 =407,9.
=407,9.
Примеры вариантов контрольной работы
Вариант 1.
В следующей выборке представлены данные по количеству Y и цене Х блага, приобретаемого домохозяйством ежемесячно в течение года:
| месяц | ||||||||||||
| Х | ||||||||||||
| Y |
По данным таблицы: а) найти линейное уравнение регрессии Y по Х и дайте интерпретацию полученного результата; б) найти с надежностью 0.95 интервальную оценку коэффициента регрессии β1 и пояснить её смысл. 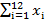 =360;
=360; 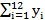 =760;
=760; 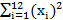 =12150;
=12150; 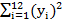 =55750;
=55750; 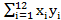 =19925.
=19925.
Вариант 2.
Имеются данные за 10 лет по прибылям Х и Y (в %) двух компаний:
| год | ||||||||||
| Х | 19.2 | 15.8 | 12.5 | 10.3 | 5.7 | 5.8 | 3.5 | 5.2 | 7.3 | 6.7 |
| Y | 20.1 | 18.0 | 10.3 | 12.5 | 6.0 | 6.8 | 2.8 | 3.0 | 8.5 | 8.0 |
По данным таблицы: а) оценить коэффициент детерминации R2 для линейного уравнения регрессии Y по Х и дайте интерпретацию полученного результата; б) найти с надежностью 0.95 интервальную оценку коэффициента регрессии β0 и пояснить её смысл. 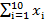 =92;
=92; 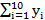 =96;
=96; 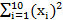 =1084.22;
=1084.22; 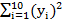 =1225.68;
=1225.68; 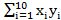 =1142.51.
=1142.51.
Вариант 3.
В следующей выборке представлены данные по количеству Y и цене Х блага, приобретаемого домохозяйством ежемесячно в течение года:
| месяц | ||||||||||||
| Х | ||||||||||||
| Y |
По данным таблицы: а) оценить тесноту и направление связи между переменными Х и Y с помощью коэффициента корреляции и дайте интерпретацию полученного результата; б) найти с надежностью 0.95 интервальную оценку остаточной дисперсии 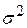 и пояснить её смысл.
и пояснить её смысл. 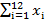 =360;
=360; 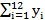 =760;
=760; 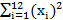 =12150;
=12150; 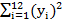 =55750;
=55750; 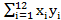 =19925.
=19925.
Вариант 4.
Имеются данные за 10 лет по прибылям Х и Y (в %) двух компаний:
| год | ||||||||||
| Х | 19.2 | 15.8 | 12.5 | 10.3 | 5.7 | 5.8 | 3.5 | 5.2 | 7.3 | 6.7 |
| Y | 20.1 | 18.0 | 10.3 | 12.5 | 6.0 | 6.8 | 2.8 | 3.0 | 8.5 | 8.0 |
По данным таблицы: а) оценить 95%-ный доверительный интервал для среднего значения прибыли компании при прибыли другой компании равной 5% для линейного уравнения регрессии Y по Х и пояснить его смысл; б) оценить с надежностью 0.95 значимость коэффициента линейной регрессии β1 и уравнения регрессии Y по Х с использованием t критерия и пояснить его смысл.
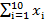 =92;
=92; 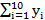 =96;
=96; 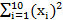 =1084.22;
=1084.22; 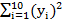 =1225.68;
=1225.68; 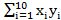 =1142.51.
=1142.51.
VI. ТЕМАТИЧЕСКИЙ ПЛАН ИЗУЧЕНИЯ ДИСЦИПЛИНЫ
| № п/п | Наименования разделов и тем | Аудиторные часы | Сам. раб. (часы, формы) | Интерактивные формы обучения | Формы текущего кон-ля | ||
| Лекции | Практ. зан. | Все-го | |||||
| Основные понятия эконометрики | |||||||
| 1.1. | Введение в дисциплину | 2, лит.[1] | |||||
| 1.2. | Основные этапы построения эконометрических моделей | 2, лит. | пдз[2] | ||||
| 2. | Элементы теории вероятностей и математической статистики в эконометрике | ||||||
| 2.1. | Основные законы распределения случайных величин | 2, лит. | |||||
| 2.2. | Зависимые и независимые случайные величины | 2, лит. | |||||
| 2.3. | Интервальные оценки | 2, лит., п.з.[3] | Комп.з.[4] | ||||
| 2.4. | Статистическая проверка гипотез | 2, лит., п.з. | Комп.з. | тест, пдз | |||
| 3. | Парная линейная регрессия | ||||||
| 3.1. | Суть регрессионного анализа | 2, лит., п.з. | |||||
| 3.2. | Метод наименьших квадратов | 2, лит., п.з. | Комп.з. | ||||
| 3.3. | Проверка качества уравнения регрессии | 2, лит., п.з. | Комп.з. | тест, пдз, к.р. | |||
| 4. | Линеаризованные регрессионные модели | ||||||
| 4.1. | Наиболее распространенные нелинейные регрессии | 4, лит., п.з. | Комп.з. | ||||
| 4.2. | Оценка параметров нелинейных моделей и проверка их качества | 4, лит., п.з. | Комп.з. | тест, пдз | |||
| 5. | Анализ одномерных временных рядов | ||||||
| 5.1. | Определение и структура временного ряда | 0,5 | 2,5 | 2, лит., п.з. | Комп.з. | ||
| 5.2. | Моделирование тенденции временного ряда | 0,5 | 2,5 | 2, лит., п.з. | Комп.з. | ||
| 5.3. | Моделирование сезонных и циклических колебаний | 4, лит., п.з. | Комп.з. | тест, пдз |
| 6. | Множественная линейная регрессия | ||||||
| 6.1. | Линейная модель множественной регрессии | 2, лит., п.з. | |||||
| 6.2. | Оценка параметров множественной регрессии методом МНК | 2, лит., п.з. | Комп.з. | ||||
| 6.3. | Проверка качества уравнения регрессии | 4, лит., п.з. | Комп.з. | тест, пдз | |||
| 7. | Нарушение условий Гаусса-Маркова. Обнаружение и устранение | ||||||
| 7.1. | Гетероскедастичность | 3, лит., п.з. | Комп.з. | ||||
| 7.2. | Автокорреляция | 3, лит., п.з. | Комп.з. | ||||
| 7.3. | Мультиколлинеарность | 2, лит., п.з. | Комп.з. | тест, пдз | |||
| 8. | Общие понятия о системах одновременных уравнений | ||||||
| 8.1 | Общие понятия о системах одновременных уравнений | 2, лит., п.з. | пдз | ||||
| КСР (контроль самост. работы студ.) | |||||||
| Итого | 30/60% | ||||||
| Экза-мен | |||||||
| Всего по дисциплине | 30/60% |
Дата добавления: 2014-12-07; просмотров: 5085;
