Раздел V. Теория вероятностей.

Тема 12. Основные понятия теории вероятностей.

1. Найдите число перестановок из 10 элементов.

2. Дайте классическое определение вероятности.

3. Выведите классическое определение вероятности из аксиом.

4. Получите формулу числа сочетаний из 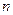элементов.

5. Для каких событий вероятность суммы равна сумме вероятностей?

6. Для каких событий вероятность произведения равна произведению вероятностей?

7. Сформулируйте теорему о полной вероятности.

Тема 13. Случайные величины и их числовые характеристики

1. Дайте определение дискретной случайной величины.

2. Дайте определение непрерывной случайной величины.

3. Приведите формулу математического ожидания дискретной случайной величины.

4. Приведите формулу математического ожидания непрерывной случайной величины.

5. Выведите свойства дисперсии, исходя из свойств математического ожидания.

Тема 14. Основные распределения случайных величин

1. Какое распределение называется биномиальным?

2. Выведите формулу Бернулли, используя теоремы теории вероятностей.

3. Чему равно приближенное значение вероятности попадания в заданный интервал биномиальной случайной величины по предельной теореме Муавра-Лапласа.

4. Запишите формулу Пуассона.

5. Среднее значение случайной величины в два раза больше дисперсии. Может ли она быть распределена по закону Пуассона?

6. Вычислите числовые характеристики равномерного, нормального и показательного распределений.