Метод интегрирования по частям в определенном интеграле

Здесь новизны еще меньше. Все выкладки статьи Интегрирование по частям в неопределенном интеграле в полной мере справедливы и для определенного интеграла.
Плюсом идёт только одна деталь, в формуле интегрирования по частям добавляются пределы интегрирования:

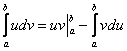
Формулу Ньютона-Лейбница здесь необходимо применить дважды: для произведения 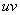и, после того, как мы возьмем интеграл .

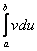Тип интеграла для примера я опять подобрал такой, который еще нигде не встречался на сайте. Пример не самый простой, но очень и очень познавательный.

Пример 8

Вычислить определенный интеграл

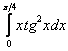
Решаем.

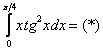
Интегрируем по частям:

У кого возникли трудности с интегралом 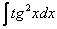, загляните на урок Интегралы от тригонометрических функций, там он подробно разобран.

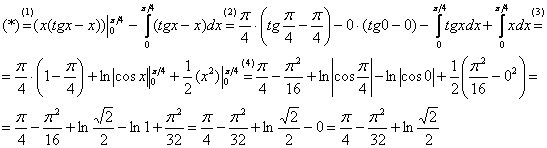
(1) Записываем решение в соответствии с формулой интегрирования по частям.

(2) Для произведения 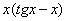применяем формулу Ньютона-Лейбница. Для оставшегося интеграла используем свойства линейности, разделяя его на два интеграла. Не путаемся в знаках!

(3) Берем два оставшихся интеграла. Интеграл

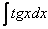также был разобран на уроке