Замена переменной в определенном интеграле

Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла. Таким образом, если с заменами у Вас не очень, следует внимательно ознакомиться с уроком Метод замены в неопределенном интеграле.

В этом параграфе нет ничего страшного или сложного. Единственная новизна состоит в вопросе, как поменять пределы интегрирования при замене.

В примерах я постараюсь привести такие типы замен, которые еще нигде не встречались на сайте.

Пример 5

Вычислить определенный интеграл

Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: 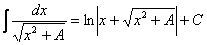. Но есть одна неувязочка, в табличном интеграле под корнем 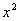, а в нашем – «икс» в четвёртой степени. Из рассуждений следует и идея замены – неплохо бы нашу четвертую степень как-нибудь превратить в квадрат. Это реально.

Сначала готовим наш интеграл к замене:

Из вышеуказанных соображений совершенно естественно напрашивается замена: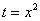
Таким образом, в знаменателе будет всё хорошо: .
Выясняем, во что превратится оставшаяся часть 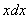подынтегрального выражения, для этого находим дифференциал :

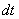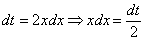
По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап.