Движение точки переменной массы
Роль ракетной техники на современном этапе цивилизации и развития механики оказалась настолько заметной, что теория движения тел с переменной массой в последние десятилетия фактически стала синонимом прикладных задач, связанных с полетом ракеты. В действительности задач о движении тела с переменной массой можно предложить очень много. Это, например, движение клети в шахте при увеличении или уменьшении длины и соответственно массы удерживающего троса; это — качение снежного кома по склону горы; это — движение падающей в воздухе дождевой капли, на поверхности которой конденсируется атмосферная влага; это — движение кометы, теряющей вблизи Солнца часть испаряющегося вещества, и многие другие задачи. Все они и им подобные уже решались в начале прошлого века, а несколько позже некоторые из них, в частности простейшие задачи о полете ракеты, вошли в учебную литературу по механике.
При решении задач о поступательном движении тела мы пользуемся теоремой об изменении количества движения, которую пишем в форме закона Ньютона:
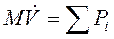 1.1
1.1
где М — масса тела, 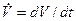 — ускорение, а в правую часть вынесена сумма проекций внешних сил. В такой же форме принято писать и уравнение для движения ракеты.
— ускорение, а в правую часть вынесена сумма проекций внешних сил. В такой же форме принято писать и уравнение для движения ракеты.
Но только в число действующих сил включается сила, создаваемая двигателем, — тяга двигателя.
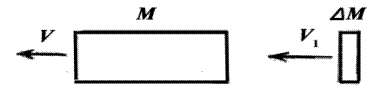
| Рис.1.1. К выводу уравнения движения тела переменной массы |
Пока, однако, забудем о ракете и подойдем к уравнению (1.1) с общих позиций. Посмотрим, что в нем изменится, если масса тела в процессе движения не остается постоянной.
Положим, масса непрерывно увеличивается. Пусть за время Δt к массе М присоединяется масса ΔМ, имеющая абсолютную скорость V1 (рис. 1.1). По теореме об изменении количества движения имеем:
до соединения масс количество движения
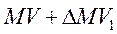 ,
,
а после того как массы объединились —
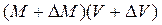 и тогда
и тогда
изменение количества движения равно импульсу внешних сил -
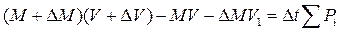
Раскрывая скобки и разделив обе части равенства на Δt, а затем, переходя к пределу, получим уравнение движения для точки переменной массы:
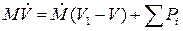 (1.2)
(1.2)
Характерной особенностью этого уравнения является то, что в него вошло слагаемое, содержащее производную от массы по времени. Значение этого слагаемого, имеющего размерность силы, зависит от относительной скорости присоединения частиц V1-V и может быть как положительным, так и отрицательным, смотря по тому, какой знак имеет относительная скорость и производная массы по времени.
|
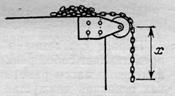
| Рис. 1.2. Пример движения тела движения тела переменной массы. |
Выведенное уравнение обладает достаточной общностью. Его можно трактовать и как векторное, и оно может быть положено в основу решения многих задач. Например, с его помощью можно подсчитать тормозящую силу, которую испытывает автомашина от действия капель при движении в потоке дождя. Для этого достаточно принять горизонтальную составляющую скорости капель V1 равной нулю, за величину V принять скорость машины, а производную от массы по времени рассматривать как суммарную массу капель, захватываемых машиной в единицу времени. С помощью уравнения (1.2) решается, например, классическая задача о сползании со стола цепи (рис. 1.2). Уравнение движения для цепи, полученное из уравнения (1.2), оказывается нелинейным, но его можно решить. При нулевой начальной скорости путь, проходимый цепью за время t, оказывается ровно в три раза меньшим, чем для свободно падающего тела.
С помощью уравнения (1.2) описывается, естественно, и движение ракеты.
Масса ракеты во времени уменьшается, и производная М меньше нуля. Это — секундный расход массы, который обозначим через 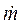 :
:
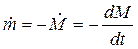 (1.3)
(1.3)
Часто вместо массового рассматривается секундный весовой расход рабочего тела
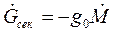
где g0 — ускорение свободно падающего тела у поверхности Земли.
Разность V1-V представляет собой относительную скорость присоединяемых частиц. Обратную ей по знаку скорость истечения обозначим буквой W:
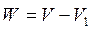
Теперь с учетом принятых обозначений уравнение движения для ракеты можно написать в виде
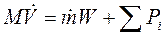 (1.4)
(1.4)
или же
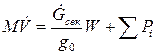
Первое слагаемое в правой части написанного выражения представляет собой реактивную силу, возникающую в результате изменения массы ракеты. Это слагаемое может рассматриваться как основная движущая сила, но это — еще не тяга двигателя.
Дата добавления: 2014-12-26; просмотров: 2301;
