Влияние силы земного тяготения

Рассмотрим простейшую задачу. Определим скорость геофи­зической ракеты, стартующей с Земли и совершающей полет по вертикали. Аэродинамическое сопротивление пока не будем рас­сматривать и ограничимся к тому же высотой подъема, в пре­делах которой ускорение тяготения g₀ можно считать постоян­ным.

В заданных условиях потеря скорости на земное тяготение очевидна. Она равна скорости, которую приобретает свободно падающее тело за время t, т. е. g₀t, и тогда

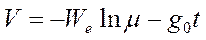
В момент выключения двигателя скорость ракеты будет

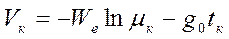(1.16)

где t_к — время, прошедшее с момента старта до выключения двигателя.

Рассматривая это выражение, можно сделать простой, но до­статочно важный вывод. Если в рассмотренных ранее идеальных условиях полета конечная скорость ракеты не зави­сит от режима расхода топлива, т. е. от времени работы двигателя и определяется лишь отношением конечной и начальной масс ракеты, то при движении в поле тяготения скорость ракеты зависит еще и от того, на сколько быстро расходуется топливо. Чем быстрее выгорит топливо, тем меньше будет время t_к, тем меньше будут потери скорости на земное тяготение.

Здесь нельзя не заметить сходства с движением лодки против течения. Чтобы выйти из стремнины, надо грести очень энергично. Если не приложить достаточных усилий, то на спокойную воду можно и вовсе не выплыть. Того же можно ожидать и от ракеты. Если расход мал и тяга недостаточна, ракета так и не оторвется от стартового устройства до тех пор, пока ее посте­пенно уменьшающийся вес не сравняется со стартовой тягой.

Идеальная скорость многоступенчатой ракеты, как мы уже видели, также не зависит от времени расходования топлива; и никакого влияния на идеальную конечную скорость не оказы­вает также и время, истекшее от момента сброса блоков преды­дущей ступени до включения двигателя последующей ступени. Но в условиях действия сил тяготения перерыв между выключе­нием и включением двигателей приводит, очевидно, к дополни­тельным потерям скорости.

Из всего сказанного можно сделать не вызывающий сомнений вывод. Чтобы уменьшить потери скорости на тяготение, следует сократить время работы двигателя t_к, т. е. быстрее сжечь весь запас топлива. Для этого надо увеличить расход. Но тогда воз­растет тяга, а ее относительная величина характеризуется уже знакомым нам параметром тяговооруженности или обратной ей величиной стартовой нагрузки на тягу (1.15)

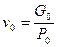
где g₀ и р_о — соответственно стартовый вес и стартовая тяга. Значит, параметр v₀ представляет собой меру длительности ра­боты двигателя и меру потерь на тяготение. С уменьшением v₀ потери на тяготение снижаются, но, к сожалению, возрастают потери иного рода.

Увеличение расхода и соответственно тяги приводит к увели­чению размеров и веса двигательной установки. В результате при неизменном полезном грузе возрастает относительный вес µ_k и уменьшается идеальная скорость, т. е. первое слагаемое в вы­ражении (1.16). Но это еще не все. При большой тяге возрастает ускорение, и растут инерционные перегрузки. Это вызывает до­полнительные заботы о прочности ракеты. Конструкцию надо усиливать, и ее вес опять же увеличивается. Высокая скорость, набранная ракетой сразу же в плотных слоях атмосферы, приве­дет к увеличению аэродинамического сопротивления. Возрастет аэродинамическая составляющая потерь. И, наконец, полет с большой скоростью в плотных слоях атмосферы связан с дополнительным нагревом конструкции. Механические характеристики легких конструкционных материалов при этом сни­жаются — отсюда новые заботы о прочности и дополнитель­ный вес.

Такого рода наглядные зависимости, когда с изменением па­раметра одни потери снижаются, а другие возрастают, неизбеж­но толкают творческую мысль на поиск оптимальных решений, в данном случае — на выбор параметра v₀. Но с этим-то как раз спешить и не следует. Зависимость между параметрами µ_к и v₀ описана нами пока лишь как иллюстрация одной из сторон сложной взаимосвязи многих параметров, характеризующих ра­кету. Для задач оптимизации должна быть, прежде всего сформулирована и обоснована цель; не в одной скорости дело. А кроме того, в дополнение к µ_к и v₀ необходимо рассмотреть и другие важные параметры, о чем мы сейчас и поговорим. Что же касается стартовой нагрузки на тягу v₀, то пока можно сказать, что ее значение для стартующих с Земли ракет-носителей естественно должно быть меньше единицы; реально оно меняется в пределах 0,5—0,75. Для второй и третьей ступеней ракет-носи­телей v₀ может оказаться и больше единицы. В этом нет пара­докса. В момент разделения ступеней ракета-носитель летит уже далеко не по вертикали, и составляющая веса вдоль вектора-скорости остается все равно меньше соответствующей состав­ляющей стартовой тяги ступени, хотя v₀ и больше единицы.

Потери скорости на тяготение составляют основную часть потерь, отличающих реальные условия выведения ракеты от рассмотренных ранее идеальных условий полета. Однако имеют­ся еще и другие виды потерь.