Характерные особенности траектории

Тяжелые боевые баллистические ракеты и ракеты-носители стартуют вертикально. Такой старт не только обладает несом­ненными преимуществами перед наклонным; он является един­ственно возможным. Тонкостенная конструкция ракеты не спо­собна противостоять боковым нагрузкам при движении и сходе с направляющих, а пусковая система при наклонном старте та­кого типа ракет по своему весу и габаритам могла бы быть сравнимой разве что с египетскими пирамидами.

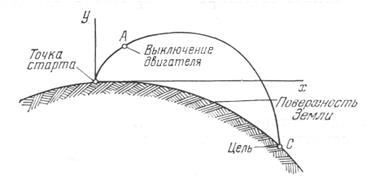
Рис.3.1. Траектория баллистической ракеты

При вертикальном старте ракета устанавливается на пуско­вом устройстве, имеющем в простейших случаях сходство с круг­лым столом, снабженным сквозным центральным проемом для выхода струи двигателя.

После старта баллистическая ракета продолжает подъем по вертикали, примерно в течение 5—15 с,после чего начинается ее разворот в сторону цели.

Траекторию баллистической ракеты (рис. 3.1) можно в пер­вом приближении рассматривать как плоскую кривую. Участок от точки старта до точки А проходится ракетой с работающим двигателем и называется активным участком, или участком вы­ведения. Та часть траектории, где ракета испытывает заметное воздействие аэродинамических сил, называется атмосферным участком полета. Для тяжелых баллистических ракет атмо­сферный участок всегда короче активного. То же самое можно сказать и о составных ракетах-носителях. Отделение блоков первой ступени производится в условиях, когда аэродинамиче­ские силы уже весьма малы.

После выключения двигателя (точка А) ракета летит как свободно брошенное тело, и вид траектории определяется только притяжением Земли и начальными условиями для этого участ­ка — координатами точки и вектором скорости в момент выклю­чения двигателя. При подходе к цели ракета входит в плотные слои атмосферы, испытывает торможение и значительный нагрев. Этот участок траектории так и называется участком входа в ат­мосферу.

Траектория выведения ракеты-носителя (рис. 3.2), например двухступенчатой,по своему характеру практически не отли­чается от траектории дальней баллистической ракеты. В точке А заканчивают работу двигатели первой ступени. Блоки первой ступени отбрасываются и падают на Землю (точка С). Вторая ступень сообщает ракете необходимую скорость, и в конце актив­ного участка, уже на орбите, двигатель выключается (точка В).

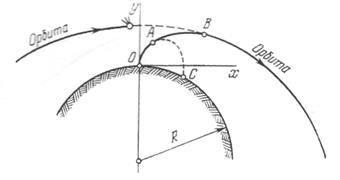
Рис.3.2. Траектория ракеты-носителя.

Разворот ракеты на участке выведения осуществляется ор­ганами управления по заранее выбранной программе. Ответ­ственность за выведение ракеты несет система управления.

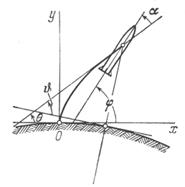
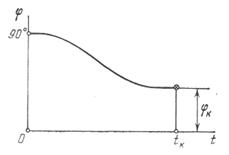
Выведение ракеты характеризуется программным углом φ — углом между осью ракеты и стартовым горизонтом (рис. 3.3). Зависимость угла φ от времени называется программой измене­ния угла тангажа. В простейших случаях для баллистических ракет относительно небольшой дальности график программы угла тангажа имеет вид кривой, показанной на рис. 3.4.

Программный угол φ близок углу наклона траектории θ (θ – угол между вектором скорости и стартовым горизонтом), но не равен ему. Между осью ракеты и касательной к траектории образуется относительно небольшой изменяющийся во времени угол α, называемый углом атаки.

Выбор способа выведения баллистической ракеты относится к классу краевых задач, когда необходимо выбрать начальные параметры программного движения при заданных условиях в конце траектории. Для боевых ракет задаются наземные коор­динаты цели. Для ракет-носителей задается высота и вектор скорости в конце участка выведения. Для космических траекторий в краевые условия входит также астрономическое время, отвечающее моменту выведения объекта.

Траектория баллистической ракеты с необходимой точностью определяется методами численного интегрирования дифферен­циальных уравнений движения. Но эта операция может быть проведена лишь при условии, когда уже известны основные пара­метры ракеты — ее весовые и тяговые характеристики, а найти их значения можно, только располагая необходимыми сведе­ниями о траектории. Возникает замкнутый круг неопределенно­стей, свойственный начальной стадии проектирования вообще любой машины, а не только ракеты-носителя.