Тяга двигателя

В ракетном двигателе струя истекающих газов формируется в сопловой, сначала сужающейся, а затем расширяющейся ча­сти камеры. Скорость текущих вдоль сопла газов постепенно на­растает, а давление соответственно падает. Возникает вопрос, где следует провести границу между отбрасываемыми газами и тем предметом, который мы будем называть ракетой.

Такое разделение можно произвести различными способами, но предпочтительным будет тот, который даст наибольшие удоб­ства для определения действующих сил.

Самое простое и очевидное — это отделить струю истекаю­щих газов по крайнему срезу сопла, а все то, что находится в пределах внешней поверхности корпуса и плоскости среза, и считать ракетой (рис. 1.3).

Отделяя мысленно, часть механической системы, мы, в со­ответствии с правилами механики, обязаны заменить действие отброшен­ной части на оставшуюся силами взаимодействия. По­скольку окружающая среда нами пока не рассматривается, мы заменяем ее действие на ракету невозмущенным атмосферным давлением р_h, распределенным по внешней поверхности. Отбра­сывая струю газов, мы также должны заменить ее действие на оставшуюся по другую сторону сечения массу давлением, которое возникает в струе на срезе сопла. Это давление принято обозначать через р_а (рис. 1.3). Оно не обязательно равно атмосферному и может быть как больше, так и меньше его.

Теперьостается условиться о том, что же следует понимать под тягой двигателя. Для ракеты это та движущая сила, перво­причину возникновения которой мы усматриваем в работе двигателя. Она обладает тем удобным свойством, что может быть непосредственно замерена на стенде (рис. 1.4).

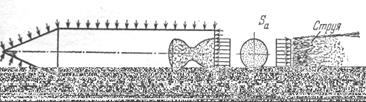
Рис. 1.3. К выводу формулы тяги.

Для закре­пленной ракеты сила тяги уравновешивается реакцией связи R, равной тяге Р . Поэтому ускорение равно нулю, и уравнение движения для точки переменной массы (1.4) примет вид

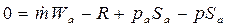
где S_a — площадь выходного сечения сопла, а W_а — скорость истечения по­тока в этом сечении.

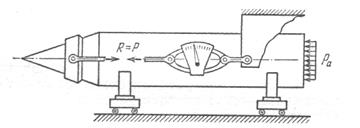
Рис. 1.4. Силы, действующие на закрепленную ракету.

Так как R = P, то тяга

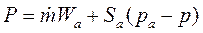
Следует особо подчеркнуть, что под давлением р понимается исключительно барометрическое давление окружающей среды, но не истинное давление на поверхности ракеты, значение и закон распределения которого зависят от условий обтекания. Все добавочные силы, связанные со скоростью полета в атмосфере, относятся к категории аэродинамических и в выражение тяги не включаются.

Выражение для тяги на высоте h получим в окон­чательном виде:

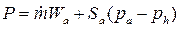(1.5)

или

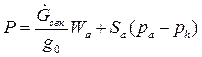
Для стартующей с поверхности Земли ракеты тяга непрерывно возрастает от своего начального значения

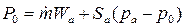
(где р_о — давление у поверхности Земли) до наибольшего зна­чения, называемого пустотной тягой —

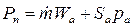(1.6)

Отличие стартовой тяги от пустотной определяется площадью выходного сечения сопла и для реальных двигателей лежит в пределах 10 — 15%.

После того как введено понятие тяги, мы получаем возмож­ность написать уравнение для поступательного движения ра­кеты в обычной форме закона Ньютона (1.1):

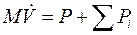
Здесь М — текущее значение массы ракеты, а под знак суммы вынесены составляющие не рассмотренных нами пока сил, та­ких как аэродинамическое сопротивление и вес ракеты.

Итак, истекающую струю газов мы отделили от ракеты пло­скостью, проходящей через выходное сечение сопла. Но как было сказано ранее, это не единственное решение. В частности, раз­деление можно произвести по внутренней поверхности камеры, заменив действие отброшенных газов на стенки камеры некото­рым изменяющимся вдоль оси давлением р_г, приводящим к воз­никновению результирующей силы Р_г (рис. 1.5). Нетрудно дога­даться, что результирующая Р_г как раз и представляет собой пустотную тягу Р_п, из которой для определения тяги на высоте h следует вычесть произведение S_ap_h,т. е.

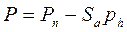(1.7)

Таким образом, пустотная тяга представляет собой резуль­тирующую сил давления, распределенных по внутренней поверх­ности камеры. В дальнейшем мы увидим, что это давление не зависит ниот скорости полета, ни от условий окружающей среды, и поэтому пустотная тяга представляет собой одну из основных характеристик собственно самого двигателя, а не условий полета.

Часто выражение тяги в пустоте записывают в форме реактивной силы

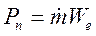(1.8)

где W_е - так называемая эффективная скорость истечения.

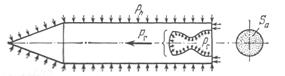
Рис.1.5. Распределение сил давления по поверхности ракеты и по внутренней поверхности камеры.

Из сопоставления выражений (1.6) и (1.8) следует, что эф­фективная скорость истечения

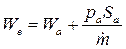(1.9)

Основной особенностью эффективной скорости истечения яв­ляется то, что она не зависит от секундного расхода 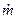, посколь­ку, как это будет показано позже, давление р_а на выходе из сопла пропорционально 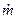, а сама скорость истечения W_a также отрасхода не зависит (правда, в некоторых определенных пре­делах). В реально существующих двигателях эффективная скорость истечения превышает действительную примерно на 10—15%.

В заключение можно отметить, что при выводе выражения тяги нами были сделаны некоторые замаскированные упроще­ния. Ускорение 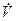закрепленной на стенде ракеты мы приняли равным нулю. Между тем центр масс ракеты вследствие сгора­ния топлива смещается. Поэтому уравнение равновесия следо­вало бы, строго говоря, заменить уравнением движения, введя производные от координаты центра масс по времени. Рассматривая пустотную тягу как равнодействующую сил внутрикамерного давления р_г, мы пренебрегли тягой, создаваемой жидким топливом при впрыске в камеру. Наконец, масса находящихся в камере газов должна либо включаться, либо не включаться в общую массу ракеты М, смотря по тому, где проводится по­верхность, отделяющая ракету от отбрасываемого рабочего тела. Учет перечисленных особенностей, однако, приводит к со­вершенно ничтожным числовым поправкам, и ими с полным основанием пренебрегают.