Находим новые переделы интегрирования.

Это достаточно просто. Смотрим на нашу замену 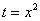и старые пределы интегрирования , .

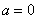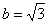Сначала подставляем в выражение замены 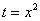нижний предел интегрирования, то есть, ноль:

Потом подставляем в выражение замены 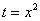верхний предел интегрирования, то есть, корень из трёх:

Готово. И всего-то лишь…

Продолжаем решение.

(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования.

(2) Это простейший табличный интеграл, интегрируем по таблице. Константу

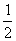
лучше оставить за скобками (можно этого и не делать), чтобы она не мешалась в дальнейших вычислениях. Справа отчеркиваем линию с указанием новых пределов интегрирования – это подготовка для применения формулы Ньютона-Лейбница.

(3) Используем формулу Ньютона-Лейбница .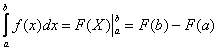

Ответ стремимся записать в максимально компактном виде, здесь я использовал свойства логарифмов.

Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену, никаких обратных замен проводить не надо.

А сейчас пара примеров для самостоятельного решения. Какие замены проводить – постарайтесь догадаться самостоятельно.

Пример 6

Вычислить определенный интеграл

Пример 7

Вычислить определенный интеграл

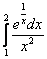
Это примеры для самостоятельного решения. Решения и ответы в конце урока.