Определенный интеграл. Как вычислить площадь фигуры
Переходим к рассмотрению приложений интегрального исчисления. На этом уроке мы разберем типовую и наиболее распространенную задачу – как с помощью определенного интеграла вычислить площадь плоской фигуры. Наконец-то все ищущие смысл в высшей математике – да найдут его. Мало ли. Придется вот в жизни приближать дачный участок элементарными функциями и находить его площадь с помощью определенного интеграла.
Для успешного освоения материала, необходимо:
1) Разбираться в неопределенном интеграле хотя бы на среднем уровне. Таким образом, чайникам для начала следует ознакомиться с уроком Неопределенный интеграл. Примеры решений.
2) Уметь применять формулу Ньютона-Лейбница и вычислять определенный интеграл. Наладить теплые дружеские отношения с определенными интегралами можно на странице Определенный интеграл. Примеры решений.
В действительности, для того чтобы находить площадь фигуры не надо так уж много знаний по неопределенному и определенному интегралу. Задание «вычислить площадь с помощью определенного интеграла» всегда предполагает построение чертежа, поэтому гораздо более актуальным вопросом будут ваши знания и навыки построения чертежей. В этой связи полезно освежить в памяти графики основных элементарных функций, а, как минимум, уметь строить прямую, параболу и гиперболу. Сделать это можно (и многим – нужно) с помощью методического материала Графики и свойства Элементарных функций.
Как обычно, весь материал изложен просто, подробно, с минимумом теории. Собственно, с задачей нахождения площади с помощью определенного интеграл все знакомы еще со школы, и мы мало уйдем вперед от школьной программы. Этой статьи вообще могло бы и не быть, но дело в том, что задача встречается в 99 случаев из 100, когда студент с увлечением осваивает курс высшей математики (мучаясь от ненавистной вышки).
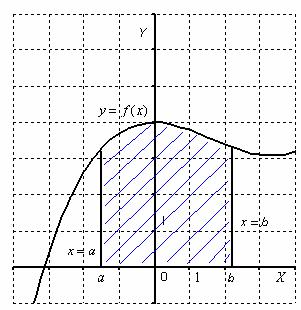
Начнем с криволинейной трапеции.
Криволинейной трапецией называется плоская фигура, ограниченная графиком некоторой функции
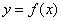 , осью
, осью 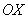
и прямыми
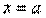 ,
, 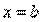 :
:
Дата добавления: 2014-11-29; просмотров: 2001;
