Вокруг оси абсцисс ; – вокруг оси ординат .

В данной статье будут разобраны оба случая. Особенно интересен второй способ вращения, он вызывает наибольшие затруднения, но на самом деле решение практически такое же, как и в более распространенном вращении вокруг оси абсцисс. В качестве бонуса я вернусь кзадаче нахождения площади фигуры, и расскажу вам, как находить площадь вторым способом – по оси 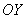. Даже не столько бонус, сколько материал удачно вписывается в тему.

Начнем с наиболее популярной разновидности вращения.

Вычисление объема тела, образованного вращением
плоской фигуры вокруг оси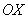

Пример 1

Вычислить объем тела, полученного вращением фигуры, ограниченной линиями 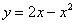, 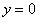вокруг оси .

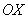Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости 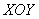необходимо построить фигуру, ограниченную линиями 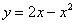, , 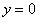при этом не забываем, что уравнение 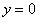задаёт ось 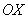. Как рациональнее и быстрее выполнить чертёж, можно узнать на страницах Графики и свойства Элементарных функцийи Определенный интеграл. Как вычислить площадь фигуры. Это китайское напоминание, и на данном моменте я больше не останавливаюсь.

Чертёж здесь довольно прост:

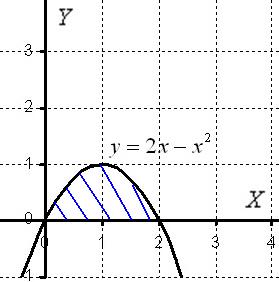
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси 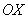. В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси 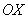. На самом деле у тела есть математическое название, но в справочнике что-то лень смотреть, поэтому едем дальше.