Как вычислить объем тела вращения?
Объем тела вращения можно вычислить по формуле:
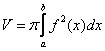
В формуле перед интегралом обязательно присутствует число 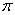 . Так повелось – всё, что в жизни крутится, связано с этой константой.
. Так повелось – всё, что в жизни крутится, связано с этой константой.
Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.
Функция 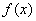 … что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболы
… что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболы 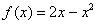 сверху. Это и есть та функция, которая подразумевается в формуле.
сверху. Это и есть та функция, которая подразумевается в формуле.
В практических заданиях плоская фигура иногда может располагаться и ниже оси 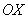 . Это ничего не меняет – функция в формуле возводится в квадрат:
. Это ничего не меняет – функция в формуле возводится в квадрат: 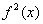 , таким образом объем тела вращения всегда неотрицателен, что весьма логично.
, таким образом объем тела вращения всегда неотрицателен, что весьма логично.
Вычислим объем тела вращения, используя данную формулу:
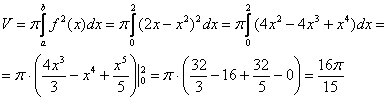
Как я уже отмечал, интеграл почти всегда получается простой, главное, быть внимательным.
Ответ: 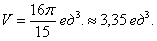
В ответе нужно обязательно указать размерность – кубические единицы 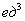 . То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубические единицы? Потому что наиболее универсальная формулировка. Могут быть кубические сантиметры, могут быть кубические метры, могут быть кубические километры и т.д., это уж, сколько зеленых человечков ваше воображение поместит в летающую тарелку.
. То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубические единицы? Потому что наиболее универсальная формулировка. Могут быть кубические сантиметры, могут быть кубические метры, могут быть кубические километры и т.д., это уж, сколько зеленых человечков ваше воображение поместит в летающую тарелку.
Пример 2
Найти объем тела, образованного вращением вокруг оси 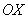 фигуры, ограниченной линиями
фигуры, ограниченной линиями 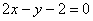 ,
, 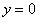 ,
, 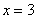
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Рассмотрим две более сложные задачи, которые тоже часто встречаются на практике.
Пример 3
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями 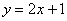 ,
, 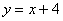 ,
, 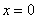 и
и 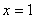
Решение:Изобразим на чертеже плоскую фигуру, ограниченную линиями 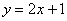 ,
, 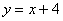 ,
, 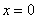 ,
, 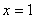 , не забывая при этом, что уравнение
, не забывая при этом, что уравнение 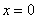 задает ось
задает ось 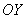 :
:
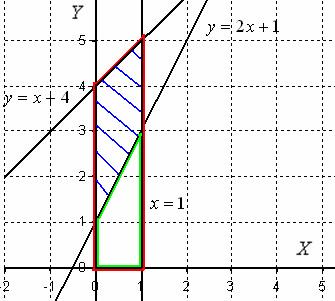
Искомая фигура заштрихована синим цветом. При её вращении вокруг оси 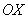 получается такой сюрреалистический бублик с четырьмя углами.
получается такой сюрреалистический бублик с четырьмя углами.
Объем тела вращения вычислим как разность объемов тел.
Сначала рассмотрим фигуру, которая обведена красным цветом. При её вращении вокруг оси 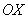 получается усеченный конус. Обозначим объем этого усеченного конуса через
получается усеченный конус. Обозначим объем этого усеченного конуса через 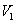 .
.
Рассмотрим фигуру, которая обведена зеленым цветом. Если вращать данную фигуру вокруг оси 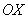 , то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через
, то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через 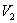 .
.
И, очевидно, разность объемов 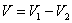 – в точности объем нашего «бублика».
– в точности объем нашего «бублика».
Используем стандартную формулу для нахождения объема тела вращения:
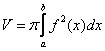
1) Фигура, обведенная красным цветом ограничена сверху прямой 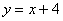 , поэтому:
, поэтому:
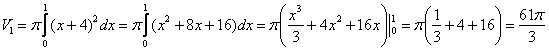
2) Фигура, обведенная зеленым цветом ограничена сверху прямой 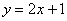 , поэтому:
, поэтому:
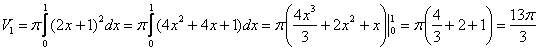
3) Объем искомого тела вращения: 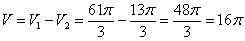
Ответ: 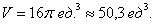
Любопытно, что в данном случае решение можно проверить, используя школьную формулу для вычисления объема усеченного конуса.
Само решение чаще оформляют короче, примерно в таком духе:
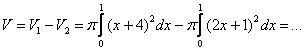
Дата добавления: 2014-11-29; просмотров: 1766;
