Интегралы от тригонометрических функций
(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.
Далее ответ доводится «до ума». Повторюсь, будьте ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫ при подстановках и заключительных вычислениях. Здесь допускают ошибки чаще всего.
Уважаемый студент, распечатай и сохрани:
Что делать, если дан определенный интеграл, который кажется сложным или не сразу понятно, как его решать?
1) Сначала находим неопределенный интеграл (первообразную функцию). Если на первом же этапе случился облом, дальше рыпаться с Ньютоном и Лейбницем бессмысленно. Путь только один – повышать свой уровень знаний и навыков в решении неопределенных интегралов.
2) Проверяем найденную первообразную функцию дифференцированием. Если она найдена неверно, третий шаг будет напрасной тратой времени.
3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО – тут самое слабое звено задания.
И, на закуску, интеграл для самостоятельного решения.
Пример 9
Вычислить определенный интеграл
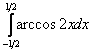
Решение и ответ где-то рядом.
Следующий рекомендуемый урок по теме – Как вычислить площадь фигуры с помощью определенного интеграла?Там речь пойдет о геометрическом смысле определенного интеграла. Дополнительные материалы по определенному интегралу также можно найти в статье Эффективные методы вычисления определенных интегралов. Данный урок содержит ряд очень важных технических приёмов и позволит существенно повысить навыки вычисления определенного интеграла.
Решения и ответы:
Пример 2: Решение:
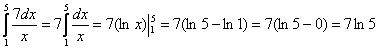
Пример 4: Решение:
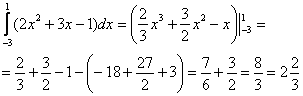
Пример 6: Решение:
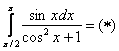
Проведем замену переменной: 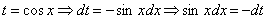 ,
,
Новые переделы интегрирования:

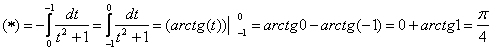
Примечания: В рассмотренном интеграле – как раз тот случай, когда уместно применить свойство определенного интеграла 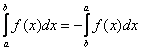 .
.
Если не совсем понятно, почему из арктангенса можно вынести минус, рекомендую обратиться к методическому материалуГрафики и свойства элементарных функций.
Пример 7: Решение:
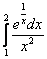
Замена: 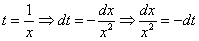
Новые пределы интегрирования:
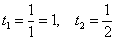
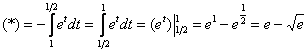
Пример 9: Решение:

Интегрируем по частям:

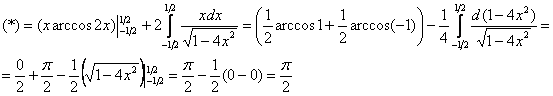
Дата добавления: 2014-11-29; просмотров: 2259;
