Построение уравнения парной регрессии

Для проверки возможности использования линейной функции определяется разность ( 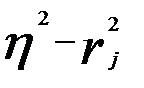); если она менее 0,1, то считается возможным применение линейной функции. В рассматриваемом примере ( 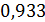-0,84)=0,036 <0,1. Значение 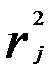определено по сгруппированным данным.

Для решения этой же задачи можно использовать величину 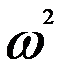, определяемую по формуле

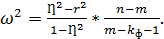(58)

где m — число групп, на которое разделен диапазон значений факторного признака.

Если 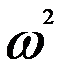окажется меньше критического значения F- критерия, то нулевая гипотеза о возможности использования в качестве уравнения регрессии линейной функции не опровергается. Значение F -критерия определяется по таблице в зависимости от уровня значимости 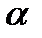= 0,05 (вероятность Р = 0,95) и числа степеней свободы знаменателя ( ) и числителя ( 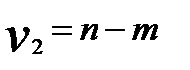) (см. функцию F.расп. EXCEL).

При линейной связи параметры ( и 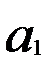) уравнения парной регрессии:

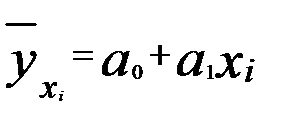(59)

находятся с помощью метода наименьших квадратов. Суть метода заключается в минимизации суммы квадратов отклонений теоритических значений результативного признака ( 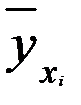) от его фактических значений ( ):

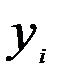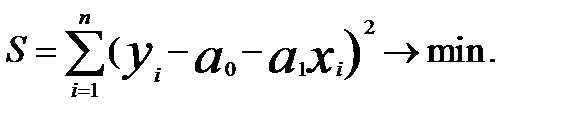(60)

Условие (7.26) выполняется при равенстве нулю частных производных по параметрам 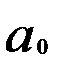и :

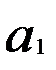(61)

Сократим каждое уравнение системы (7.27) на (-2), раскроем скобки и получим следующую систему нормальных уравнений:

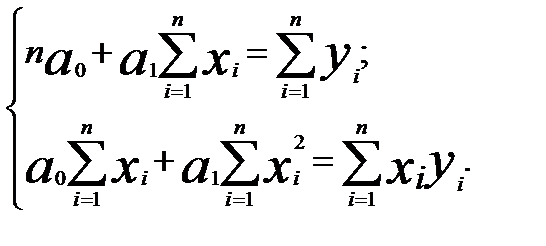(62)

Поделим каждое уравнение системы (7.28) на объём статистической совокупности (n), тогда упомянутую систему можно представить в более наглядном виде:

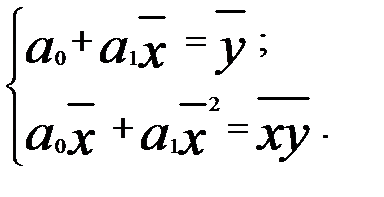(63)

Из первого уравнения системы (63) следует, что:

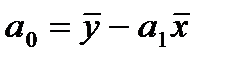=-30,19 (64) Подставив полученное выражение во второе уравнение, получим:

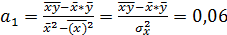(65)

Коэффициент корреляции определяется по формуле:

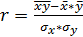=0,984 (66)

Учитывая (65) и (66) получим

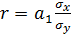(67)

или 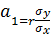(68) Зная значения r, и 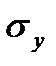можно вычислить по выражениям (68) и (64) параметры 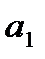и 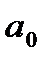линейного уравнения регрессии.

Параметр 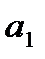, нельзя использовать для непосредственной оценки влияния факторного признака на результативный при­знак из-за различия единиц измерения исследуемых показате­лей. Для этих целей вычисляют значение среднего коэффициента эластичности и бета-коэффициент:

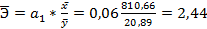(69)

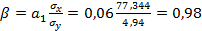(70)

Коэффициент эластичности показывает, на сколь­ко процентов изменяется результативный признак у при изменении факторного признака x на один процент.

Бета-коэффициент показывает, на какую часть своего среднего квадратического отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину своего среднего квадратического отклонения.