Анализ зависимости таможенных платежей от внешнеторгового оборота фирм
4.1 Построение групповой таблицы.
Для построения групповой таблицы вычисляются средние значения результативного признака в каждой группе фирм (графа 6 табл. 5.2). Сравнив их значения, можно предположить о наличии прямой корреляционной зависимости между признаками, что иллюстрируется рис. 4.
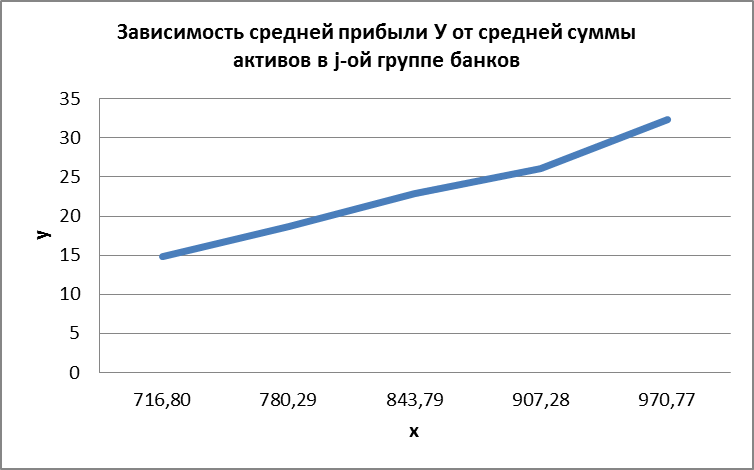
Рис. 4. Зависимость средней прибыли У от средней суммы активов в j-ой группе банков
4.2. Проверка правила сложения дисперсий и оценка степени влияния факторного признака на величину результативного.
Правило сложения дисперсий заключается в равенстве общей дисперсии сумме средней из внутригрупповых и межгрупповой дисперсий, т.е.:
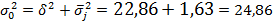 , (44)
, (44)
Где 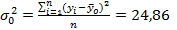 , (45)
, (45)
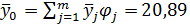 — общая средняя арифметическая результативного признака;
— общая средняя арифметическая результативного признака;
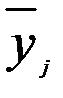 _ среднее значение результативного признака в
_ среднее значение результативного признака в 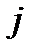 - ой группе;
- ой группе;
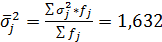 - cредняя из внутригрупповых дисперсий;
- cредняя из внутригрупповых дисперсий;
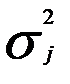 —дисперсия в j-ой группе (графа 13 табл. 5.2), вычисляемая по формуле:
—дисперсия в j-ой группе (графа 13 табл. 5.2), вычисляемая по формуле:
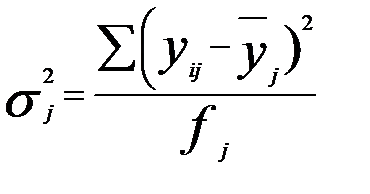 ;
;
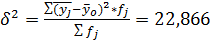 - межгрупповая дисперсия;
- межгрупповая дисперсия;
Как следует из выражения (44) правило сложения дисперсий выполняется.
Разделив левую и правую части выражения (44) на общую дисперсию получим следующее тождество:
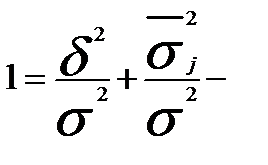 доли средней из внутригрупповых и межгрупповой дисперсий в сумме равны единице.
доли средней из внутригрупповых и межгрупповой дисперсий в сумме равны единице.
Второе слагаемое именуется эмпирическим коэффициентом детерминации (причинности) и обозначается 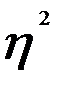
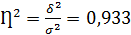 (46)
(46)
Квадратный корень из коэффициента детерминации принято называть корреляционным отношением:
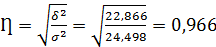 (47)
(47)
Изменяется корреляционное отношение от 0 до 1.
При недостаточном количестве данных в выделенных группах к рассчитанной величине корреляционного отношения вносится поправка:
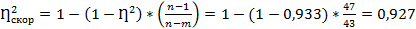 ;
; 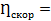 0,962 (48)
0,962 (48)
где m — число выделенных групп.
Для оценки значимости корреляционного отношения можно применить однофакторный дисперсионный анализ. Его логика рассуждений сводится к следующему:
Пусть 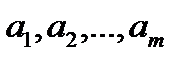 - математическое ожидание результативного признака, соответственно в группах
- математическое ожидание результативного признака, соответственно в группах 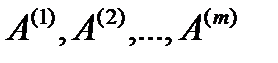 . Если при изменении уровня фактора групповые математические ожидания не изменяются, то результативный признак не зависит от фактора А - в противном случае такая зависимость имеется.
. Если при изменении уровня фактора групповые математические ожидания не изменяются, то результативный признак не зависит от фактора А - в противном случае такая зависимость имеется.
В связи с тем, что числовые значения математических ожиданий неизвестны, то возникает задача проверки гипотезы
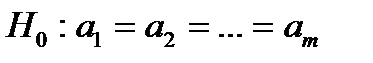
Проверить данную гипотезу можно при соблюдении следующих требований при каждом значении уровня фактора:
1. наблюдения независимы и проводятся в одинаковых условиях;
2. результативный признак имеет нормальный закон распределения с постоянной для различных уровней генеральной дисперсией.
Для ответа на второй вопрос вычислим значения относительных показателей асимметрии и эксцесса ta= 1,14; te=1,42 для зависимой переменной. Учитывая, что каждый из них меньше 1,5 эмпирическое распределение таможенных платежей в бюджет не противоречит нормальному.
Проверим выполнение гипотезы:
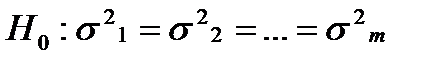 (49)
(49)
с помощью критерия Бартлетта:
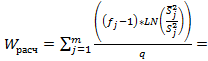 3,976
3,976
где 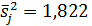 остаточная дисперсия, что является синонимом средней из внутригрупповых выборочных дисперсий;
остаточная дисперсия, что является синонимом средней из внутригрупповых выборочных дисперсий;
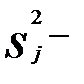 выборочная дисперсия в
выборочная дисперсия в 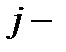 ой группе (графа 14 табл. 5.2); ;
ой группе (графа 14 табл. 5.2); ; 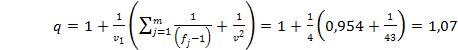
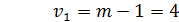
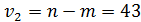 .
.
При выполнении гипотезы о равенстве дисперсий, величина w имеет распределение близкое к 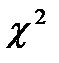 с
с 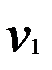 степенями свободы.
степенями свободы.
При соблюдении условия
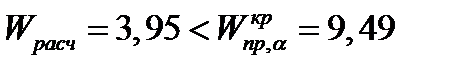 гипотеза (7.14) подтверждается.
гипотеза (7.14) подтверждается.
Здесь 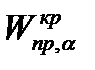 - правосторонняя критическая точка при заданном уровне значимости
- правосторонняя критическая точка при заданном уровне значимости 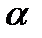 , определяющая критический интервал (
, определяющая критический интервал ( 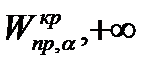 ).
).
Далее можно приступить к проверке гипотезы 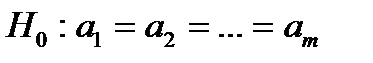 . Для этого сформируем массив значений результативного признака по группам (табл. 8).
. Для этого сформируем массив значений результативного признака по группам (табл. 8).
Таблица 8
| группа 1 | группа 2 | группа 3 | группа 4 | группа 5 |
| 12,62 | 17,38 | 20,38 | 24,76 | 31,47 |
| 12,37 | 17,52 | 23,12 | 25,26 | 32,44 |
| 12,82 | 17,35 | 22,32 | 25,72 | 33,21 |
| 15,47 | 17,75 | 22,67 | 27,13 | |
| 15,82 | 19,35 | 22,45 | 25,7 | |
| 15,64 | 17,94 | 22,43 | 27,93 | |
| 14,45 | 19,54 | 21,88 | ||
| 14,04 | 18,1 | 21,96 | ||
| 14,37 | 19,63 | 22,21 | ||
| 18,12 | 19,42 | 23,14 | ||
| 16,74 | 19,93 | 22,54 | ||
| 18,96 | 23,99 | |||
| 19,75 | 24,86 | |||
| 25,58 | ||||
| 24,7 |
Обратимся к режиму работы «Однофакторный дисперсионный анализ».
| Однофакторный дисперсионный анализ | |||||||||||
| ИТОГИ | |||||||||||
| Группы | Размер выборки | Сумма | Среднее | Дисперсия | |||||||
| группа 1 | 162,46 | 14,76909 | 3,24331 | ||||||||
| группа 2 | 242,62 | 18,66308 | 0,99784 | ||||||||
| группа 3 | 344,23 | 22,94867 | 1,8011 | ||||||||
| группа 4 | 156,5 | 26,08333 | 1,44275 | ||||||||
| группа 5 | 97,12 | 32,37333 | 0,76023 | ||||||||
| Дисперсионный анализ | |||||||||||
| Источник вариации | SS | df | MS | F | P-Значение | F критическое | |||||
| Между группами | 1097,586 | 274,3965 | 150,58117 | 1,07E-24 | 2,588836 | ||||||
| Внутри групп | 78,35674 | 1,82225 | |||||||||
| Итого | 1175,942 | ||||||||||
Проверка гипотезы о равенстве математических ожиданий основывается на сравнении оценок факторной 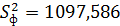 и остаточной
и остаточной 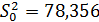 дисперсий. В математической статистике доказывается, что если гипотеза о равенстве математических ожиданий подтверждается, то величина
дисперсий. В математической статистике доказывается, что если гипотеза о равенстве математических ожиданий подтверждается, то величина
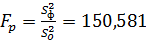 имеет F – распределения с числом свободы
имеет F – распределения с числом свободы 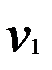 и
и 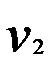 , т.е.
, т.е.
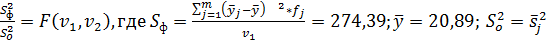
При использовании F – критерия строится правосторонняя область ( 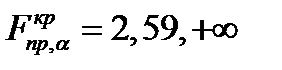 ), т.к. обычно
), т.к. обычно 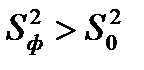 . Если расчетное значение F – критерия
. Если расчетное значение F – критерия 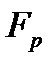 попадает в указанный интервал, то гипотеза о равенстве групповых математических ожиданий отвергается, т.е. считаем, что фактор А влияет на результативный признак Y и можно измерить степень этого влияния с помощью корреляционного отношения.
попадает в указанный интервал, то гипотеза о равенстве групповых математических ожиданий отвергается, т.е. считаем, что фактор А влияет на результативный признак Y и можно измерить степень этого влияния с помощью корреляционного отношения.
Дата добавления: 2014-11-29; просмотров: 1796;
