Проверка адекватности модели
Проверка значимости осуществляется на основе t – критерия Стьюдента, т.е. проверяется гипотеза о том, что параметр, измеряющий связь, равен нулю.
Средняя ошибка параметра 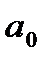 равна:
равна:
 , (76)
, (76)
а для параметра 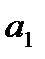 :
:
. 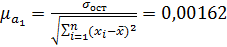 (77)
(77)
Расчетные значения t- критерия вычисляются по формуле:
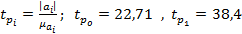 (78) Параметр считается значимым, если
(78) Параметр считается значимым, если  . Значение
. Значение  определяется по формуле СТЬЮДЕНТ.ОБР(0,95;46) при числе степеней свободы
определяется по формуле СТЬЮДЕНТ.ОБР(0,95;46) при числе степеней свободы 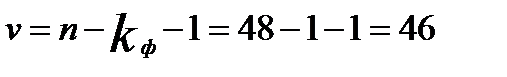 и с вероятностью (Р=1-
и с вероятностью (Р=1- 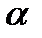 ) При
) При 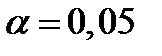 и
и 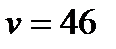
 . Следовательно, в рассматриваемом примере параметры
. Следовательно, в рассматриваемом примере параметры 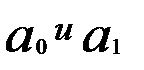 являются значимыми.
являются значимыми.
Параметр  лежит в пределах
лежит в пределах 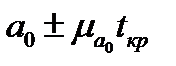 ;(
;(  ,
,
а параметр 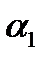 -
-  ;
; 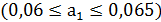 .
.
Значимость уравнения регрессии в целом определяется с помощью F – критерия Фишера:
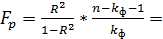 279,49 (79)
279,49 (79)
Расчетное значение F сопоставляется с критическим 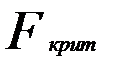 для числа степеней свободы
для числа степеней свободы 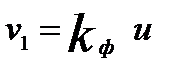
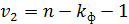 при заданном уровне значимости
при заданном уровне значимости 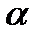 (например,
(например, 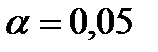 ), где
), где 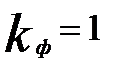 ,
, 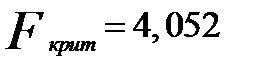 .
.
Если 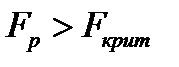 , то уравнение считается значимым.
, то уравнение считается значимым.
Другой подход к определению значений параметров уравнения парной регрессии и оценке значимости заключается в обращении к режиму “РЕГРЕССИЯ” EXCEL. Следует отметить, что результаты расчётов, приведенные в табл.7-9, получены с меньшими временными затратами и полностью совпадают с результатами “ручного” счёта.
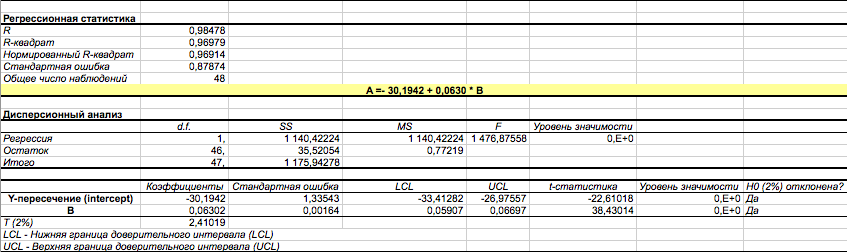
| Остатки | |||
| Наблюдение | Предсказанное Y | Остаток | Стандартные остатки |
| 12,97821 | -0,35821 | -0,41205 | |
| 13,15971 | -0,78971 | -0,9084 | |
| 13,2284 | -0,4084 | -0,46979 | |
| 13,66199 | 1,80801 | 2,07975 | |
| 14,62053 | 1,19947 | 1,37974 | |
| 14,6407 | 0,9993 | 1,14949 | |
| 14,97975 | -0,52975 | -0,60937 | |
| 15,18772 | -1,14772 | -1,32022 | |
| 15,21167 | -0,84167 | -0,96817 | |
| 16,13619 | 1,98381 | 2,28197 | |
| 16,65485 | 0,08515 | 0,09795 | |
| 17,41425 | -0,03425 | -0,03939 | |
| 17,58314 | -0,06314 | -0,07263 | |
| 17,99719 | -0,64719 | -0,74446 | |
| 18,00412 | -0,25412 | -0,29232 | |
| 18,5524 | 0,7976 | 0,91747 | |
| 18,94439 | -1,00439 | -1,15535 | |
| 19,19837 | 0,34163 | 0,39298 | |
| 19,23492 | -1,13492 | -1,30549 | |
| 19,39562 | 0,23438 | 0,2696 | |
| 19,42461 | -0,00461 | -0,0053 | |
| 19,74854 | 0,18146 | 0,20873 | |
| 19,85441 | -0,89441 | -1,02884 | |
| 20,6762 | -0,9262 | -1,06541 | |
| 21,23583 | -0,85583 | -0,98446 | |
| 21,34738 | 1,77262 | 2,03904 | |
| 21,67508 | 0,64492 | 0,74184 | |
| 21,83201 | 0,83799 | 0,96394 | |
| 22,0488 | 0,4012 | 0,4615 | |
| 22,21643 | 0,21357 | 0,24566 | |
| 22,5996 | -0,7196 | -0,82775 | |
| 22,633 | -0,673 | -0,77415 | |
| 23,03507 | -0,82507 | -0,94908 | |
| 23,08171 | 0,05829 | 0,06705 | |
| 23,49954 | -0,95954 | -1,10375 | |
| 23,61487 | 0,37513 | 0,43152 | |
| 23,95266 | 0,90734 | 1,04371 | |
| 24,25327 | 1,32673 | 1,52613 | |
| 24,95595 | -0,25595 | -0,29442 | |
| 25,02275 | -0,26275 | -0,30224 | |
| 25,1532 | 0,1068 | 0,12285 | |
| 26,45206 | -0,73206 | -0,84209 | |
| 27,45661 | -0,32661 | -0,3757 | |
| 27,60408 | -1,90408 | -2,19026 | |
| 27,71311 | 0,21689 | 0,24949 | |
| 29,97493 | 1,49507 | 1,71978 | |
| 32,09873 | 0,34127 | 0,39256 | |
| 32,98543 | 0,22457 | 0,25832 |
Проверка наличия или отсутствия систематической ошибки
1. Проверка свойства нулевого среднего.
Рассчитывается среднее значение ряда остатков:
. 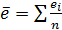 ==-0,0000208 (80)
==-0,0000208 (80)
Если оно близко к нулю, то считается, что модель не содержит систематической ошибки и адекватна по критерию нулевого среднего, иначе – модель неадекватна по данному критерию. Если средняя ошибка не точно равна нулю, то для определения степени ее близости к нулю используется t – критерий Стьюдента. Расчётное значение критерия вычисляется по формуле
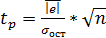 (81)
(81)
и сравнивается с критическим 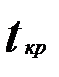 .Если выполняется неравенство
.Если выполняется неравенство 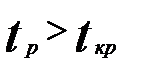 , то модель неадекватна по данному критерию.
, то модель неадекватна по данному критерию.
2. Проверка случайности ряда остатков.
Осуществляется по методу серий. Серией называется последовательность расположенных подряд значений ряда остатков, для которых разность  (графа 4 табл. 7.4) имеет один и тот же знак, где
(графа 4 табл. 7.4) имеет один и тот же знак, где 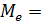 -0,020 - медиана ряда остатков, значение которой рассчитано по данным графы 3 упомянутой таблицы
-0,020 - медиана ряда остатков, значение которой рассчитано по данным графы 3 упомянутой таблицы
Если модель хорошо отражает исследуемую зависимость, то она часто пересекает линию графика исходных данных и тогда серий много, а их длина невелика. Иначе – серий мало и некоторые из них включают большое число членов.
В качестве серий рассматриваются расположенные подряд ошибки с одинаковыми знаками. Далее подсчитывается число серий 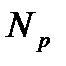 и длина максимальной из них
и длина максимальной из них  . Полученные значения сравниваются с критическими
. Полученные значения сравниваются с критическими
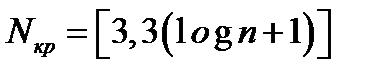 (82)
(82) 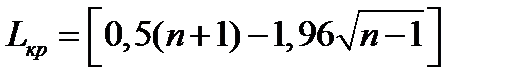 (83) (квадратные скобки означают округление вниз до ближайшего целого).
(83) (квадратные скобки означают округление вниз до ближайшего целого).
Если выполняется система неравенств:
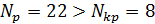
 (84)
(84)
то модель признается адекватной по критерию случайности, если хотя бы одно из неравенств нарушено, то модель признается неадекватной по данному критерию.
3. Проверка независимости последовательных остатков.
Является важнейшим критерием адекватности модели и осуществляется с помощью коэффициента Дарбина-Уотсона:
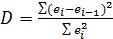 =1,66 (85)
=1,66 (85)
Для рядов с тесной взаимосвязью между последовательными значениями остатков значение  близко к нулю, что свидетельствует о том, что закономерная составляющая не полностью отражена в модели и частично закономерность присуща ряду остатков, т.е. модель неадекватна исходному процессу.
близко к нулю, что свидетельствует о том, что закономерная составляющая не полностью отражена в модели и частично закономерность присуща ряду остатков, т.е. модель неадекватна исходному процессу.
Если последовательные остатки независимы, то  близко к 2. Это свидетельствует о хорошем качестве модели и чистой фильтрации закономерной составляющей.
близко к 2. Это свидетельствует о хорошем качестве модели и чистой фильтрации закономерной составляющей.
При отрицательной автокорреляции остатков (строго периодичном чередовании их знаков)  близко к 4.
близко к 4.
Для проверки существенности положительной автокорреляции остатков значение  сравнивается с
сравнивается с 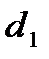 и
и 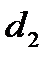 из табл. 2 Приложения к лекции:
из табл. 2 Приложения к лекции:
· если  , то гипотеза о независимости остатков отвергается и модель признается неадекватной по критерию независимости остатков;
, то гипотеза о независимости остатков отвергается и модель признается неадекватной по критерию независимости остатков;
· если  , то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию (в рассматриваемом примере
, то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию (в рассматриваемом примере 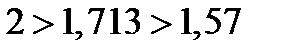 );
);
· если 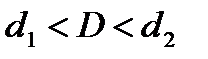 , то значение критерия лежит в области неопределенности.
, то значение критерия лежит в области неопределенности.
Если 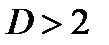 , то возникает предположение об отрицательной автокорреляции остатков, и тогда с критическими значениями сравниваются не
, то возникает предположение об отрицательной автокорреляции остатков, и тогда с критическими значениями сравниваются не  , а
, а  и делаются аналогичные выводы.
и делаются аналогичные выводы.
4. Проверка постоянства дисперсии остатков.
Если на графике остатков они укладываются в симметричную относительно нулевой линии полосу шириной 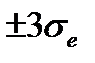 (модуль стандартных остатков меньше 3) и не имеют как положительной так и отрицательной тенденций, то дисперсии ошибок наблюдений можно считать постоянными.
(модуль стандартных остатков меньше 3) и не имеют как положительной так и отрицательной тенденций, то дисперсии ошибок наблюдений можно считать постоянными.
Значения стандартных остатков вычисляются по формуле
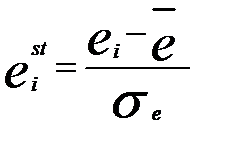 , где
, где  и приведены в графе 5 табл.7.4.
и приведены в графе 5 табл.7.4.
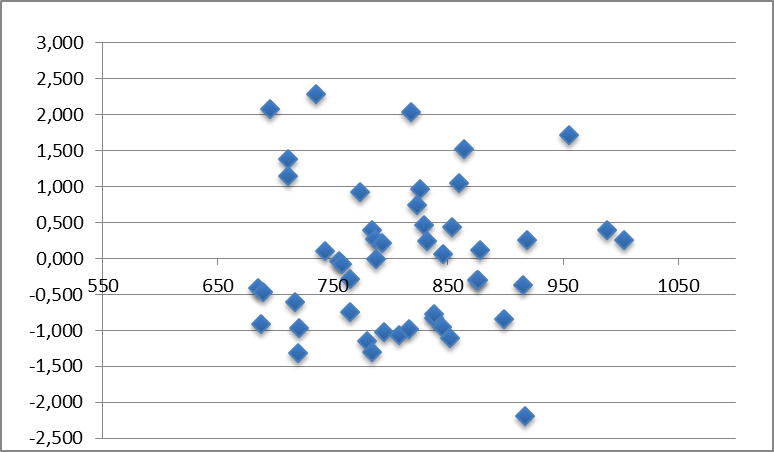
Рис. 7.3 График стандартных остатков
Кроме визуальной оценки постоянства дисперсии существуют и более точные методы, например, тест Гольдфельда-Квандта. Суть теста заключается в следующем. Все n наблюдений упорядочиваются по возрастанию значений независимой переменной (x) и производится оценка параметров регрессий для первых 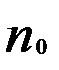 и последних
и последних 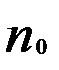 наблюдений с помощью метода наименьших квадратов. Для наибольшей мощности теста рекомендуется выбирать значение
наблюдений с помощью метода наименьших квадратов. Для наибольшей мощности теста рекомендуется выбирать значение 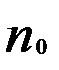 порядка n/3. Далее вычисляется расчётное значение статистики Фишера
порядка n/3. Далее вычисляется расчётное значение статистики Фишера
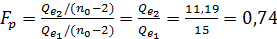 , (86)
, (86)
где 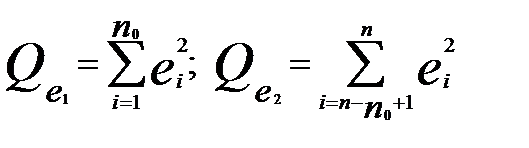 - суммы квадратов остатков для первых
- суммы квадратов остатков для первых 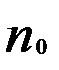 и последних
и последних 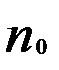 наблюдений соответственно. Далее задаётся уровень значимости
наблюдений соответственно. Далее задаётся уровень значимости 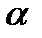 и определяется
и определяется  с помощъю статистических таблиц.
с помощъю статистических таблиц.  .
.
Если 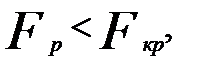 то делается вывод о постоянстве дисперсии.
то делается вывод о постоянстве дисперсии.
По совокупности четырех критериев делается вывод о принципиальной возможности использования модели: если модель адекватна по критериям постоянства дисперсий и нулевого среднего и хотя бы по одному из двух других критериев, то она может быть принята для использования, хотя и не признается полностью адекватной.
Дата добавления: 2014-11-29; просмотров: 1762;
