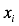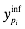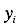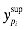Построение доверительных интервалов

Конечной целью моделирования является оценка или прогнозирование показателя Y в зависимости от значений X.

Прогноз подразделяется на точечный и интервальный и обычно осуществляется не более чем на одну треть размаха:

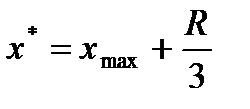=1002,52+317,47/3=1108,34

где 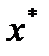- точка прогноза.

В точечном прогнозе показателя Y для 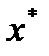определяется лишь одно число, которое представляет условное среднее и (при выполнении предпосылок регрессионного анализа) наиболее вероятное значение с точки зрения закономерности, отраженной в модели. В таком прогнозе не учитываются отклонения от закономерностей в результате воздействия случайных и неучтенных факторов.

В интервальном прогнозе отклонения от закономерностей в результате случайных воздействий определяются границами доверительных интервалов.

Доверительным интервалом называется такой интервал, которому с заданной степенью вероятности (называемой доверительной) принадлежат истинные значения показателя при условии, что закономерности, отраженные в модели, не противоречат развитию как на участке наблюдения, так и на участке оценки (или в периоде упреждения прогноза).

Случайные отклонения от модели проявляются в виде ошибок. Поэтому при определении границ, доверительных интервалов необходимо определить из чего складываются возможные ошибки моделирования, оценки и прогнозирования. При условии, что модель адекватна, и возможные ошибки носят случайный характер, следует различать два основных источника ошибок:

1. ошибки аппроксимации (рассеяние наблюдений относительно модели);

2. ошибки оценок параметров модели.

Наличие ошибок первого типа очевидно даже визуально. Величина ошибок аппроксимации характеризуется остаточной дисперсией 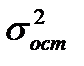или средней квадратической ошибкой 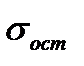. Распределение этих ошибок для адекватных моделей – нормально (нормальность ошибок – одно из условий адекватности).

Ошибки оценок параметров модели обусловлены тем, что их параметры, фиксированные в модели как однозначные, в действительности являются случайными величинами, так как они оцениваются на основе фактических данных, в которых присутствует как закономерная, так и случайная составляющие. Средние значения этих оценок при выполнении предпосылок регрессионного анализа соответствует истинным значениям параметров, а их дисперсии зависят от остаточной дисперсии, числа наблюдений и вида модели.

Общее среднее квадратическое отклонение истинных значений от расчетных может быть представлено как:

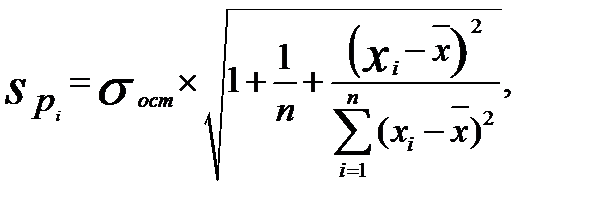(87)

а в точке прогноза:

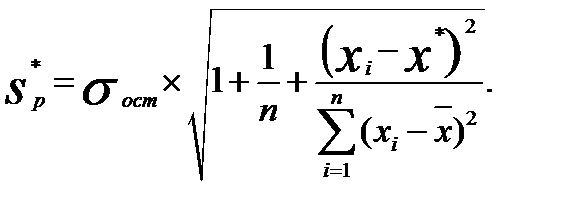= 1,0132 (88)

Исходя из предпосылки нормального распределения остатков границы доверительных интервалов определяются по формулам:

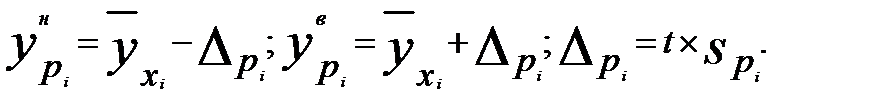(89)

Анализ выражений позволяет для моделей парной регрессии сделать вывод, что доверительные интервалы тем шире, чем:

- больше остаточная дисперсия (менее точна модель);

- значение 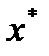больше удалено от среднего значения

- сложнее форма модели;

- больше заданная доверительная вероятность.

Обобщая полученные результаты, можно сделать вывод, что построенная модель обладает хорошим качеством, т.е. она достаточно точна и адекватна исследуемому процессу по всем перечисленным ранее критериям. Учитывая еще и нормальность ряда остатков можно осуществлять точечный и интервальный прогнозы. В связи с этим табл. 7.5 приведены данные для построения доверительных интервалов.

	685,05	11,132	12,62	12,965	14,798	1,833
	687,93	11,316	12,37	13,147	14,977	1,831
	689,02	11,385	12,82	13,215	15,045	1,830
	695,9	11,824	15,47	13,649	15,474	1,825
	711,11	12,791	15,82	14,607	16,422	1,815
	711,43	12,812	15,64	14,627	16,442	1,815
	716,81	13,154	14,45	14,966	16,778	1,812
	720,11	13,364	14,04	15,174	16,984	1,810
	720,49	13,388	14,37	15,198	17,008	1,810
	735,16	14,319	18,12	16,122	17,925	1,803
	743,39	14,841	16,74	16,641	18,440	1,799
	755,44	15,605	17,38	17,400	19,194	1,795
	758,12	15,775	17,52	17,569	19,362	1,794
	764,69	16,191	17,35	17,982	19,774	1,792
	764,8	16,198	17,75	17,989	19,781	1,792
	773,5	16,748	19,35	18,538	20,327	1,790
	779,72	17,141	17,94	18,929	20,718	1,788
	783,75	17,396	19,54	19,183	20,971	1,788
	784,33	17,432	18,1	19,220	21,007	1,788
	786,88	17,593	19,63	19,380	21,168	1,787
	787,34	17,622	19,42	19,409	21,197	1,787
	792,48	17,947	19,93	19,733	21,520	1,787
	794,16	18,053	18,96	19,839	21,625	1,786
	807,2	18,875	19,75	20,661	22,446	1,786
	810,661875	19,109		20,894	22,680	1,786
	816,08	19,434	20,38	21,220	23,006	1,786
	817,85	19,546	23,12	21,332	23,117	1,786
	823,05	19,873	22,32	21,659	23,445	1,786
	825,54	20,030	22,67	21,816	23,602	1,786
	828,98	20,246	22,45	22,033	23,819	1,787
	831,64	20,413	22,43	22,200	23,987	1,787
	837,72	20,796	21,88	22,583	24,371	1,788
	838,25	20,829	21,96	22,617	24,405	1,788
	844,63	21,230	22,21	23,019	24,808	1,789
	845,37	21,276	23,14	23,065	24,854	1,789
		21,692	22,54	23,483	25,274	1,791
	853,83	21,807	23,99	23,598	25,389	1,791
	859,19	22,143	24,86	23,936	25,729	1,793
	863,96	22,442	25,58	24,236	26,031	1,794
	875,11	23,141	24,7	24,939	26,737	1,798
	876,17	23,207	24,76	25,006	26,804	1,799
	878,24	23,337	25,26	25,136	26,935	1,799
	898,85	24,626	25,72	26,435	28,244	1,809
	914,79	25,621	27,13	27,439	29,257	1,818
	917,13	25,766	25,7	27,586	29,406	1,820
	918,86	25,874	27,93	27,695	29,516	1,821
	954,75	28,109	31,47	29,956	31,804	1,848
	988,45	30,200	32,44	32,079	33,959	1,879
	1002,52	31,071	33,21	32,966	34,860	1,894
	1108,34	38,651		39,632	40,614	2,346

Массив 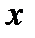дополнен двумя значениями: и , которые выделены жирным шрифтом. Значения: 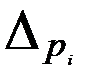- ширина доверительного интервала; - нижняя граница доверительного интервала; 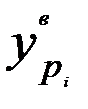- верхняя граница доверительного интервала вычислены по формулам (7.53) с доверительной вероятностью 0,95 и соответствующим ей коэффициентом доверия Стьюдента 2,315. Выбор распределения Стьюдента обусловлен достаточно большим значением относительного показателя асимметрии остатков.

График доверительных интервалов и график их ширины приведены на рис. 7.4 и 7.5.

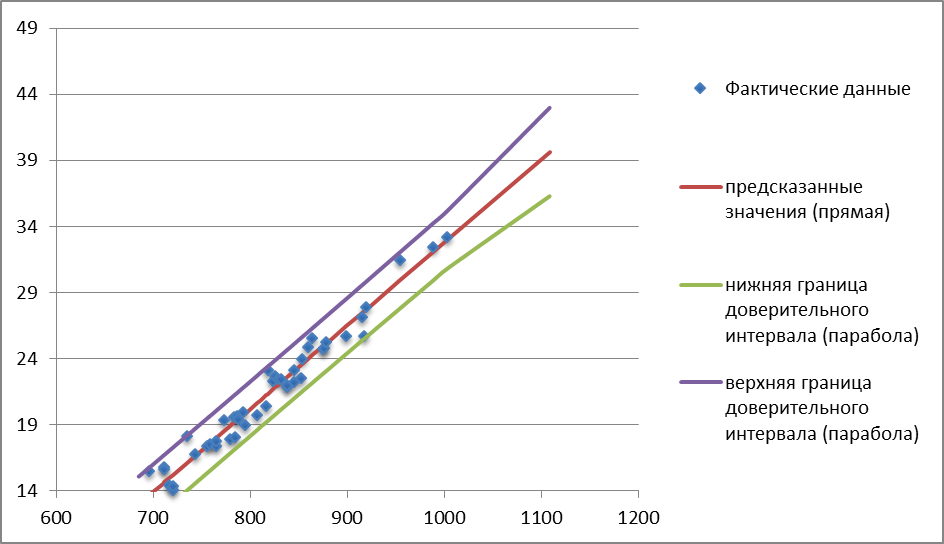
Рис. 7.4 График доверительных интервалов

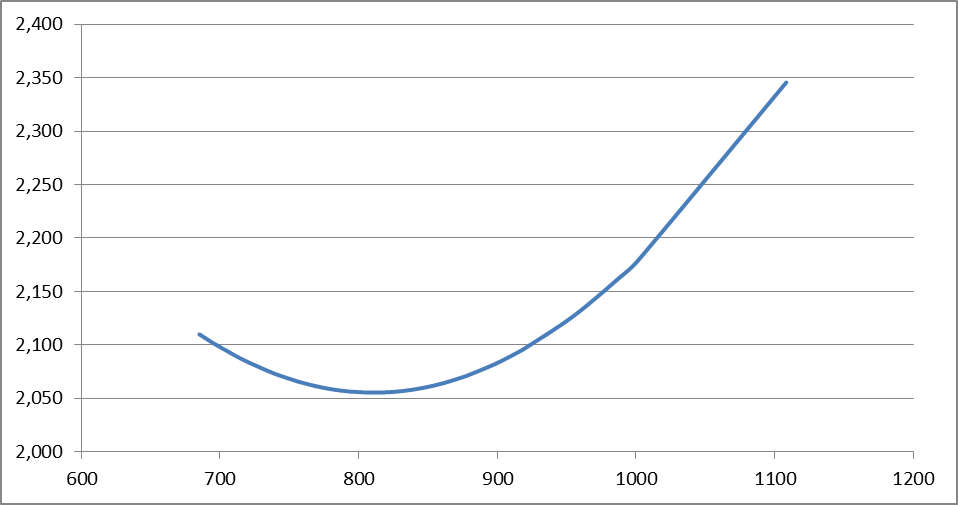
Рис. 7.5 График ширины доверительных интервалов

С учетом нормального распределения остатков при среднем значении активов банков равном 1108,34 млн. руб. с вероятностью 0,95 прогнозируемая прибыль банков за квартал составят от 38,6 до 40,61 млн. руб., при этом условное среднее (наиболее вероятный объём поступлений) ожидается 39,63 млн. руб.