Оценка степени взаимной согласованности между суммой

Внешнеторгового оборота фирм и величиной таможенных платежей в бюджет с помощью линейного коэффициента корреляции, проверка его значимости и возможности использования линейной функции в качестве формы уравнения

Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции ( 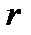); при любой форме зависимости (линейной и криволинейной) - эмпирическое корреляционное отношение ( )).

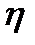Для расчета линейного коэффициента корреляции можно использовать формулу:

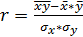=0,785, (50)

где 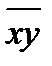— среднее значение произведения факторного и результативного признаков;

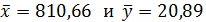- средние значения факторного и результативного признаков;

n— число единиц в совокупности;

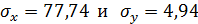— средние квадратические отклонения соответственно признака - фактора и результативного признака.

Оценка существенности линейного коэффициента корреляции при большом объеме выборки (свыше 500) проводится с использованием отношения коэффициента корреляции ( 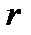) к его средней квадратической ошибке ( ):

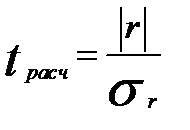, (51)

где . (52)

Если это отношение окажется больше критического значения t-критерия Стьюдента, определяемого по формуле СТЬЮДЕНТ.ОБР(0,95;46) при числе степеней свободы к = п — 2 и с вероятностью (1 — 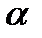), то следует говорить о существенности коэффициента корреляции ( 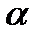— уровень значимости 0,01 или 0,05).

При недостаточно большом объеме выборки величину средней квадратической ошибки коэффициента корреляции определяют по формуле

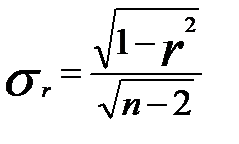. (53)

В этом случае 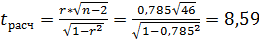. (54)

Полученная величина 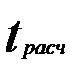сравнивается с критическим значением t-критерия Стьюдента ( ).

Так как рассчитанное значение, (tр(8,59)>tкрит(2,01), гипотеза 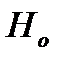:r=0 отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между суммой активов банков и величиной их прибыли.

При недостаточном объеме выборки для построения доверительного интервала коэффициент корреляции преобразуют в величину 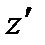, имеющую приблизительно нормальное распределение и рассчитываемую по формуле

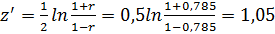. (55)

Данное выражение имеет название «z – преобразование Фишера».

Интервальная оценка для z определяется из выражения

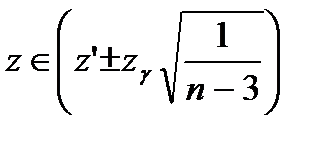(56)

где 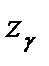- табулированые значения для стандартного нормального распределения, зависимые от 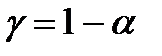. На основе обратного 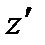преобразования Фишера определяется интервальная оценка линейного коэффициента корреляции.

Приведем реализацию изложенного алгоритма.

· по формуле ФИШЕР( 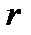) – вычисляется значение ;

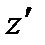· по формулам

2,44-НОРМСТОБР((0,95+1)/2)*КОРЕНЬ(1/45)=2,15 и

2,44+НОРМСТОБР((0,95+1)/2)*КОРЕНЬ(1/45)=2,73 рассчитываются интервальные оценки z;

· по формулам ФИШЕРОБР(2,25)=0,973 и ФИШЕРОБР(2,73)=0,99 находим обратные преобразования Фишера.

Таким образом, с вероятностью 0,95 линейный коэффициент корреляции заключен в интервале от 0,766 до 1,35 со стандартной ошибкой 0,09.

Проверка возможности использования линейной функции в качестве формы уравнения заключается в определении разности квадратов 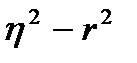, если она меньше 0,1, то считается возможным использовать линейное уравнение корреляционной зависимости. В данном случае эта разность составляет 0,036