Доверительный интервал 3 страница
В задачах 311-330 даны линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Найти частное решение, удовлетворяющее указанным начальным условиям.
-
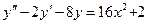 ,
, 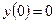 ,
,  .
. -
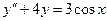 ,
, 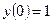 ,
, 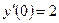 .
. -
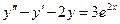 ,
, 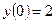 ,
,  .
. -
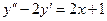 ,
, 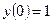 ,
, 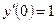 .
. -
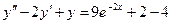 ,
, 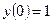 ,
, 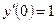 .
. -
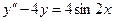 ,
,  ,
,  .
. -
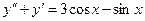 ,
, 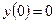 ,
, 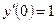 .
. -
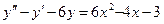 ,
, 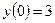 ,
,  .
. -
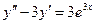 ,
,  ,
,  .
. -
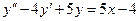 ,
, 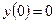 ,
,  .
. -
 ,
, 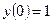 ,
, 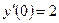 .
. -
 ,
, 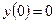 ,
, 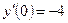 .
. -
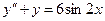 ,
,  ,
,  .
. -
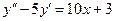 ,
,  ,
,  .
. -
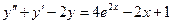 ,
, 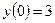 ,
,  .
. -
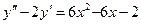 ,
, 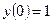 ,
, 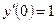 .
. -
 ,
, 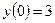 ,
,  .
. -
 ,
, 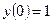 ,
,  .
. -
 ,
, 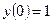 ,
, 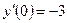 .
. -
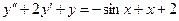 ,
, 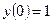 ,
, 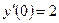 .
.
В задачах 331-340 исследовать сходимость рядов, пользуясь признаком сходимости Даламбера.
-
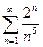 .
. -
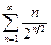 .
. -
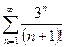 .
. -
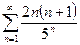 .
. -
 .
. -
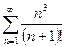 .
. -
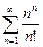 .
. -

-
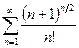 .
. -
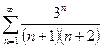 .
.
В задачах 341-350 исследовать сходимость рядов, пользуясь интегральным признаком сходимости Коши.
-
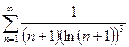 .
. -
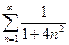 .
. -
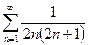 .
. -
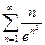 .
. -
 .
. -
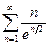 .
. -
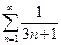 .
. -
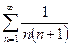 .
. -
 .
. -
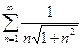 .
.
В задачах 351-370 дан степенной ряд
 .
.
Написать первые четыре члена ряда, найти интервал сходимости ряда и выяснить вопрос о сходимости ряда на концах интервала. Значения a, b и k даны.
-
 .
. -
 .
. -
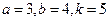 .
. -
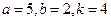 .
. -
 .
. -
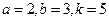 .
. -
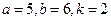 .
. -
 .
. -
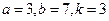 .
. -
 .
. -
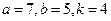 .
. -
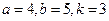 .
. -
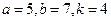 .
. -
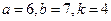 .
. -
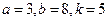 .
. -
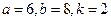 .
. -
 .
. -
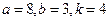 .
. -
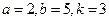 .
. -
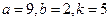 .
.
371. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что: а) студент знает все три вопроса; б) только два вопроса; в) только один вопрос экзаменационного билета.
372. В каждой из двух урн находятся 5 белых и 10 черных шаров. Из первой урны во вторую переложили неудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черным.
373. Три стрелка в одинаковых и независимых условиях производили по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из стрелков попадает в цель; б) только два стрелка попадут в цель; в) все три стрелка попадут в цель.
374. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 1600 испытаниях событие наступит 1200 раз.
375. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе – 0,95, третье – 0,85. Найти вероятность того, что при аварии сработает: а) только одно устройство; б) только два устройства; в) все три устройства.
376. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,02. Найти вероятность того, что в 150 испытаниях событие наступит 5 раз.
377. В партии из 1000 изделий имеются 10 дефектных. Найти вероятность того, что среди 50 изделий, наудачу взятых из этой партии, ровно три окажутся дефектными.
378. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 125 испытаниях событие наступит не менее 75 и не более 90 раз.
379. На трех станках при одинаковых и независимых условиях изготовляют детали одного наименования. На первом станке изготовляют 10%, на втором – 30, на третьем – 60% всех деталей. Вероятность каждой детали быть бездефектной равна 0,7, если она изготовлена на первом станке, 0,8, - если на втором станке, и 0,9, - если на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.
380. Два брата входят в состав двух спортивных команд, состоящих из 12 человек каждая. В двух урнах имеются по 12 билетов с номерами от 1до 12. Члены каждой команды вынимают наудачу по одному билету из определенной урны (без возвращения). Найти вероятность того, что оба брата вытащат билет номер 6.
- Студент разыскивает нужную формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором, третьем справочнике соответственно равна 0,6; 0,7; 0,8. Найти вероятность того, что формула содержится:
а) только в одном справочнике;
б) только в двух справочниках;
в) во всех трех справочниках.
- Брошено три игральных кости. Найти вероятность следующих событий:
а) на каждой из выпавших граней появится 5 очков;
б) на всех выпавших гранях появится одинаковое число очков.
- Число грузовых автомашин, проезжающих по шоссе, на которой стоит бензоколонка, относится к числу легковых, проезжающих по тому же шоссе, как 2:3. Известно, что в среднем одна из тридцати грузовых и две из пятидесяти легковых машин подъезжают к бензоколонке для заправки. Чему равна вероятность того, что:
а) к бензоколонке подъехала грузовая машина, и она будет заправляться;
б) к бензоколонке подъехала легковая машина, и она будет заправляться;
в) подъехавшая к бензоколонке машина будет заправляться.
- В НИИ работают 120 человек, из них 70 знают английский язык, 60 – немецкий, а 50 знают оба. Какова вероятность того, что выбранный наудачу сотрудник не знает ни одного иностранного языка.
- В первой группе студентов 15 юношей и 10 девушек, во второй – 12 юношей и 13 девушек. Из каждой группы выбирают по одному студенту. Найти вероятность того, что среди выбранных студентов хотя бы один юноша.
- В мастерской на трех станках изготавливаются однотипные детали. Вероятность безотказной работы первого станка равна 0,8, второго – 0,7, третьего – 0,9. Вероятность изготовления бракованной детали на первом станке равна 0,2, на втором – 0,3, на третьем – 0,1. Найти вероятность того, что наугад выбранная деталь окажется стандартной.
- Имеется 10 одинаковых по виду урн, из которых в 9 находятся по 2 черных и 2 белых шара, а в одной 5 белых и 1 черный шар. Из наугад взятой урны извлечен один шар. Чему равна вероятность того, что этот шар взят из урны, содержащей 5 белых шаров, если он оказался белым?
- В урне лежит 1 шар, с равной вероятностью белый или черный. В урну положили белый шар. Шары тщательно перемешаем, затем из урны извлекли один шар. Он оказался белым. Какова вероятность того, что в урне остался белый шар.
- В каждой из двух урн находится 5 белых и 10 черных шаров. Из первой урны во вторую переложили 2 шара, а затем из второй урны наудачу извлекли один шар. Найти вероятность того, что вынутый шар окажется черным.
- Путешественник, заблудившийся в лесу, вышел на поляну, откуда вело 5 дорог. Известно, что вероятность выхода из леса за час для различных дорог соответственно равны: 0,6; 0,3; 0,2; 0,1; 0,1. Чему равна вероятность того, что заблудившийся пошел по первой дороге, если известно, что он вышел из леса за час?
В задачах 391-400 задан закон распределения случайной величины Х (в первой строке таблицы даны возможные значения величины Х, а во второй строке указаны вероятности этих возможных значений). Требуется найти: 1) математическое ожидание М(Х); 2) дисперсию D(Х); 3) среднее квадратическое отклонение σ.
| Х | ||||
| Р | 0,1 | 0,2 | 0,3 | 0,4 |
| Х | ||||
| Р | 0,3 | 0,2 | 0,2 | 0,3 |
| Х | ||||
| Р | 0,2 | 0,3 | 0,1 | 0,4 |
| Х | ||||
| Р | 0,1 | 0,6 | 0,2 | 0,1 |
| Х | ||||
| Р | 0,1 | 0,5 | 0,2 | 0,2 |
| Х | ||||
| Р | 0,1 | 0,3 | 0,2 | 0,4 |
| Х | ||||
| Р | 0,3 | 0,2 | 0,2 | 0,3 |
| Х | ||||
| Р | 0,1 | 0,3 | 0,2 | 0,4 |
| Х | ||||
| Р | 0,1 | 0,6 | 0,2 | 0,1 |
| Х | ||||
| Р | 0,5 | 0,1 | 0,3 | 0,1 |
В задачах 401-405 случайная величина x задана функцией распределения
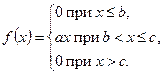
Требуется найти: 1) коэффициент a; 2) математическое ожидание М(Х); 3) дисперсию D(Х) и среднее квадратическое отклонение σ.
- b=1, c=3.
- b=2, c=4.
- b=3, c=5.
- b=4, c=6.
- b=5, c=7.
В задачах 406-410 случайная величина x задана функцией распределения

Требуется найти: 1) коэффициент a; 2) математическое ожидание М(Х); 3) дисперсию D(Х) и среднее квадратическое отклонение σ.
- b=1, c=3.
- b=2, c=4.
- b=3, c=5.
- b=4, c=6.
- b=5, c=7.
В задачах 411-430 заданы результаты обследования.
Требуется:
1) получить вариационный ряд и построить гистограмму относительных частот;
2) вычислить выборочную среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, ошибку средней;
3) с надежностью 95% указать доверительный интервал для оценки генеральной средней.
- Из стада коров-первотелок произведена случайная выборка. Получено 25 вариант удоя коров за 1 день лактации (в л):
20,9; 21,6; 8,0; 13,4; 18,3; 15,3; 12,0; 15,9; 18,5; 19,1; 20,6;
11,5; 7,7; 13,1; 18,0; 15,0; 11,7; 15,6; 18,1; 18,8; 15,0; 11,8;
8,1; 13,5; 14,4.
- Даны результаты взвешивания (в кг) 20 кроликов в возрасте 2 лет:
4,8; 5,5; 5,8; 5,1; 7,1; 5,4; 5,2; 5,4; 4,6; 5,2; 4,9; 6,4; 4,7;
5,8; 5,5; 3,8; 6,7; 3,3; 6,0; 4,7.
- Даны результаты измерения живой массы 20 телят холмогорских помесей при рождении (в кг):
38, 36, 32, 36, 30, 36, 36, 39, 32, 23, 32, 30, 34, 30, 28,
31, 24, 28, 27, 26.
- Из стада коров произведена случайная выборка. Получено 20 вариант удоя коров за 300 дней лактации (в ц):
35,9; 25,9; 35,9; 40,9; 34,2; 35,3; 35,3; 38,8; 35,5; 30,8;
42,7; 33,4; 33,7; 44,1; 38,4; 45,2; 27,0; 38,6; 37,4; 31,3.
- Даны результаты обследования 100 коров по числу отелов:
4, 8, 10, 6, 8, 6, 10, 8, 10, 6, 12, 12, 12, 14, 12, 14, 12, 8, 12,
10, 4, 8, 10, 10, 10, 8, 14, 10, 8, 12, 10, 14, 10, 4, 8, 10, 8, 12,
12, 8, 16, 10, 14, 14, 10, 12, 12, 10, 8, 10, 8, 16, 8, 10, 12, 10,
12, 8, 12, 10, 10, 12, 6, 10, 12, 6, 12, 8, 14, 12, 8, 10, 10, 6, 6,
10, 8, 12, 10, 10, 8, 10, 8, 12, 8, 10, 8, 10, 8, 12, 12, 8, 10, 10,
10, 14, 12, 8, 14, 8.
- Даны измерения длины тела у 54 экземпляров плотвы оз (в мм):
138, 139, 138, 144, 143, 138, 142, 140, 139,
140, 139, 137, 136, 135, 135, 136, 136, 136,
137, 138, 138, 137, 139, 139, 139, 140, 140,
139, 140, 140, 139, 140, 137, 141, 130, 137,
141, 141, 142, 142, 143, 143, 141, 147, 146,
146, 139, 140, 138, 140, 138, 138, 140, 143.
- Из стада коров-первотелок произведена выборка. Получены 50 вариант удоя коров за 1 день лактации (в кг):
16,9; 17,4; 17,5; 14,6; 16,5; 17,9; 14,9; 15,2; 17,3; 16,9;
13,2; 16,2; 14,6; 14,3; 15,1; 15,9; 11,3; 17,7; 16,8; 15,7;
18,7; 16,8; 13,1; 15,1; 14,9; 15,3; 15,9; 16,6; 14,8; 15,9;
11,7; 13,6; 18,2; 11,6; 13,9; 14,1; 15,2; 15,4; 15,3; 14,8;
15,3; 18,5; 17,4; 13,4; 11,2; 13,8; 12,6; 13,5; 13,8; 12,9.
- Даны результаты взвешивания (в кг) 50 коров, случайным образом отобранных из стада:
550, 550, 551, 551, 550, 551, 562, 550, 562, 551,
530, 542, 535, 542, 539, 537, 543, 540, 556, 546,
556, 556, 534, 548, 533, 558, 560, 558, 548, 540,
541, 551, 549, 551, 550, 552, 568, 538, 551, 547,
552, 559, 557, 546, 552, 550, 557, 547, 552, 554.
- Даны результаты измерения длины хвоста у оленьих мышей в возрасте одного года (в мм):
60,7; 61,2; 60,9; 61,3; 61,1; 61,0; 61,5; 61,3; 61,9; 61,4;
61,6; 61,0; 61,7; 61,1; 60,9; 61,5; 61,6; 61,4; 61,4; 61,2;
61,6; 61,3; 61,8; 61,1; 61,7; 62,3; 62,5; 62,8; 62,6; 60,9;
61,5; 61,7; 62,3; 62,3; 62,2; 61,7; 62,3; 62,5; 62,8; 62,6;
62,1; 62,6; 61,6; 62,5; 62,4; 62,1; 62,3; 62,2; 62,3; 62,2.
- Даны результаты измерения длины тела у 50 экземпляров плотвы оз (в мм):
50, 52, 140, 138, 165, 162, 210, 165, 170, 142,
63, 68, 150, 170, 168, 163, 105, 110, 112, 131,
83, 85, 125, 126, 135, 148, 102, 110, 115, 118,
92, 99, 125, 121, 118, 130, 133, 141, 182, 199,
98, 205, 127, 132, 135, 105, 119, 115, 125, 124.
- Из стада коров произведена случайная выборка. Получено 100 вариант удоя коров за 1 день лактации (в кг):
25, 29, 28, 25, 30, 29, 28, 28, 30, 27,
28, 32, 30, 32, 30, 33, 31, 33, 33, 31,
30, 29, 34, 30, 34, 31, 26, 26, 34, 27,
28, 26, 28, 30, 26, 33, 29, 31, 30, 27,
29, 33, 29, 24, 29, 31, 32, 29, 31, 32,
32, 30, 25, 30, 33, 28, 26, 28, 34, 31,
30, 32, 36, 34, 30, 32, 30, 31, 29, 30,
35, 29, 30, 28, 37, 30, 32, 32, 30, 31,
30, 28, 33, 30, 31, 26, 31, 30, 29, 26,
27, 30, 35, 29, 27, 28, 30, 32, 27, 27.
- Даны результаты измерения живого веса 100 телят холмогорских помесей при рождении (в кг):
19, 25, 29, 31, 27, 29, 29, 27, 29, 23,
29, 29, 31, 27, 33, 37, 33, 29, 31, 31,
39, 31, 27, 37, 29, 31, 25, 31, 29, 27,
29, 25, 31, 29, 31, 29, 29, 23, 33, 29,
31, 29, 27, 31, 29, 23, 33, 35, 27, 29,
29, 25, 29, 29, 33, 29, 35, 29, 25, 29,
27, 27, 23, 31, 29, 35, 29, 27, 29, 27,
31, 29, 29, 35, 25, 29, 27, 29, 31, 25,
29, 27, 31, 29, 27, 35, 31, 29, 27, 27,
21, 19, 31, 27, 29, 27, 29, 31, 31, 29.
- Даны результаты обследования гнёзд лесной ласточки Iridoprocne bicolor по количеству птенцов (шт):
4, 5, 4, 5, 5, 4, 5, 4, 3, 5, 4, 5, 6, 1, 6, 4, 4, 4, 5, 5, 3, 5, 5, 4,
6, 4, 6, 2, 3, 4, 5, 5, 5, 5, 5, 5, 4, 5, 5, 6, 4, 6, 2, 5, 5, 3, 5, 5,
5, 4, 6, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 4, 6, 7, 6, 3, 5, 5, 6, 5,
5, 4, 4, 2, 4, 4, 6, 2, 6, 5, 4, 5, 5, 5, 5, 5, 4, 5, 4, 6, 5, 4, 7, 5,
5, 5, 6, 6, 4, 4, 4, 6, 5, 4, 3, 5, 5, 7, 5, 5, 5, 5, 4, 3, 7, 6, 4, 4.
- Из стада коров-первотелок произведена случайная выборка. Получено 20 вариант удоя коров за 1 день лактации (в кг):
9,3; 20,9; 13,5; 21,6; 25,1; 15,3; 14,2; 12,0; 15,2; 15,0;
9,6; 20,6; 13,8; 11,5; 25,3; 15,0; 14,5; 11,7; 11,0; 11,8.
- Обследовано 20 телят холмогорских помесей. Их живая масса при рождении равна:
43, 26, 35, 36, 33, 26, 35, 35, 32, 28,
35, 32, 28, 36, 31, 45, 32, 32, 37, 32.
- Даны результаты измерений длины правого уха у 60 овец валахской породы (в см):
12, 10, 14, 14, 13, 12, 12, 12, 15, 13, 11, 12, 12, 14, 12,
11, 13, 12, 13, 14, 11, 13, 14, 12, 13, 12, 12, 14, 12, 14,
13, 13, 12, 13, 12, 13, 12, 11, 11, 12, 13, 14, 12, 14, 13,
14, 13, 12, 14, 15, 10, 11, 10, 11, 15, 11, 16, 11, 11, 11.
- Даны результаты измерения роста (в см) случайно отобранных 50 студентов:
177, 166, 172, 166, 161, 165, 176, 167, 165, 160,
168, 164, 167, 172, 158, 160, 170, 158, 167, 158,
159, 166, 161, 168, 173, 169, 166, 166, 163, 173,
167, 163, 158, 173, 156, 166, 164, 163, 164, 181,
170, 156, 173, 167, 168, 165, 168, 164, 166, 169.
- Даны результаты измерения живого веса телят холмогорских помесей при рождении (в кг):
27, 32, 32, 31, 32, 28, 37, 35, 26, 28,
32, 39, 34, 30, 37, 26, 27, 40, 35, 37,
28, 43, 26, 35, 45, 26, 35, 32, 32, 35,
35, 28, 32, 36, 32, 36, 37, 33, 28, 31,
36, 33, 33, 28, 23, 26, 34, 32, 36, 27,
32, 39, 30, 30, 36, 38, 24, 32, 30, 31.
- Даны результаты взвешивания 50 кроликов в возрасте 2 лет (в кг):
4,49; 4,45; 4,63; 4,79; 4,68; 4,63; 4,55; 4,51; 4,46; 4,45;
4,68; 4,71; 4,55; 4,13; 4,55; 4,43; 4,63; 4,54; 4,36; 4,54;
4,55; 4,62; 4,66; 4,77; 4,69; 4,52; 4,57; 4,12; 4,57; 4,52;
4,63; 4,78; 4,42; 4,45; 4,65; 4,43; 4,62; 4,55; 4,42; 4,28;
4,69; 4,73; 4,52; 4,49; 4,79; 4,66; 4,48; 4,49; 4,32; 4,17.
- Из стада коров-первотелок произведена случайная выборка. Получено 30 вариант удоя коров за 1 день лактации (в л):
20,6; 8,0; 19,7; 13,4; 14,5; 18,3; 17,7; 15,9; 11,1; 18,5;
20,0; 19,1; 20,9; 7,7; 20,0; 13,1; 14,8; 18,0; 18,0; 15,6;
11,3; 18,1; 20,3; 18,8; 14,0; 8,1; 12,0; 13,5; 22,0; 14,4.
Приложения
Таблица 1.
Значения функции  .
.
| х | ||||||||||
| 0,0 | 0,3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,2420 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0,0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,0044 | |||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 |
Дата добавления: 2014-12-05; просмотров: 2773;
