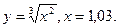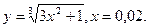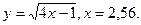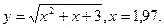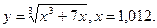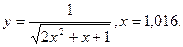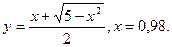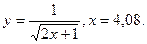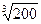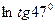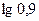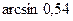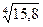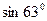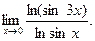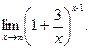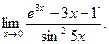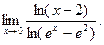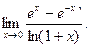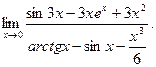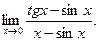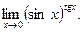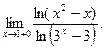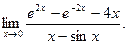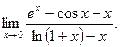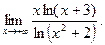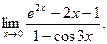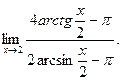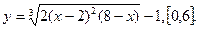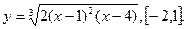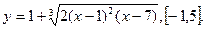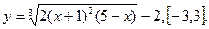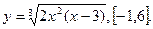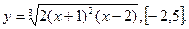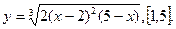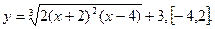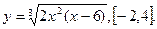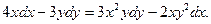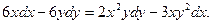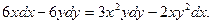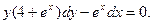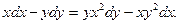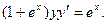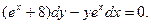Доверительный интервал 2 страница
В задачах 121-140 найти производные 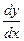 , пользуясь формулами дифференцирования.
, пользуясь формулами дифференцирования.
- а)
 ; б)
; б)  .
. - а)
 ; б)
; б) 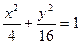 .
. - а)
 ; б)
; б) 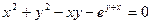 .
. - а)
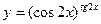 ; б)
; б) 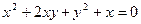 .
. - а)
 ; б)
; б) 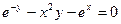 .
. - а)
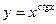 ; б)
; б)  .
. - а)
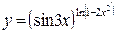 ; б)
; б)  .
. - а)
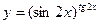 ; б)
; б) 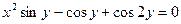 .
. - а)
 ; б)
; б)  .
. - а)
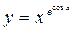 ; б)
; б) 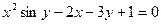 .
. - а)
 ; б)
; б) 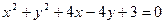 .
. - а)
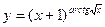 ; б)
; б) 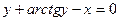 .
. - а)
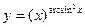 ; б)
; б) 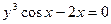 .
. - а)
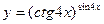 ; б)
; б) 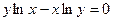 .
. - а)
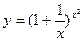 ; б)
; б) 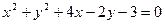 .
. - а)
 ; б)
; б) 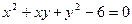 .
. - а)
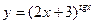 ; б)
; б)  .
. - а)
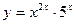 ; б)
; б) 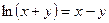 .
. - а)
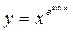 ; б)
; б) 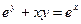 .
. - а)
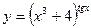
 ; б)
; б) 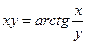 .
.
В задачах 141-150 вычислить приближенное значение функции в заданной точке.
В задачах 151-160 вычислить приближенное значение указанных величин с помощью дифференциалов соответствующих функций.
В задачах 161-180 найти 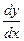 и
и 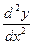 .
.
- а)
 б)
б) 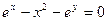 .
. - а)
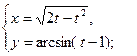 б)
б)  .
. - а)
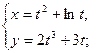 б)
б) 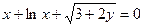 .
. - а)
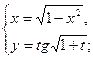 . б)
. б) 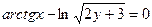
- а)
 б)
б) 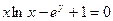
- а)
 б)
б) 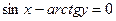 .
. - а)
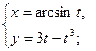 б)
б) 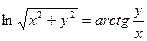 .
. - а)
 б)
б) 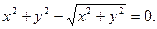
- а)
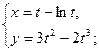 б)
б) 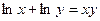 .
. - а)
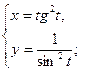 б)
б) 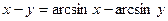 .
. - а)
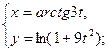 б)
б)  .
. - а)
 б)
б) 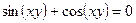 .
. - а)
 б)
б) 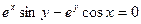 .
. - а)
 б)
б)  .
. - а)
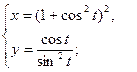 б)
б)  .
. - а)
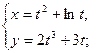 б)
б) 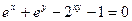 .
. - а)
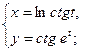 б)
б)  .
. - а)
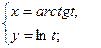 б)
б)  .
. - а)
 б)
б) 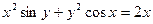 .
. - а)
 б)
б)  .
.
В задачах 181-200 вычислить предел функции по правилу Лопиталя.
В задачах 201-220 исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
-
 .
. -
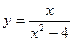
-

-
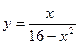
-
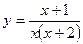
-
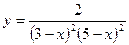
-
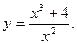
-
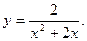
-
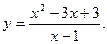
-
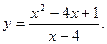
-
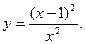
-
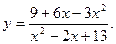
-
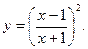
-
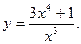
-

-
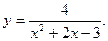
-
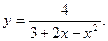
-

-
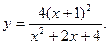
-

В задачах 221-230 найти наибольшее и наименьшее значения функций на заданных отрезках.
- Требуется изготовить из жести ведро без крышки данного объема V, цилиндрической формы. Каковы должны быть высота цилиндра и радиус основания, чтобы на изготовление ведра ушло наименьшее количество материала
- Равнобедренный треугольник, вписанный в окружность радиуса R. вращается вокруг прямой, которая проходит через его вершину параллельно основанию. Какова должна быть высота этого треугольника, чтобы тело, полученное в результате его вращения, имело наибольший объем?
- Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R.
- При каких линейных размерах закрытая цилиндрическая банка данной вместимости V будет иметь наименьшую полную поверхность.
- Требуется изготовить коническую воронку с образующей равной 20 см. Какова должна быть высота воронки, чтобы ее объем был наибольшим.
- Требуется огородить забором прямоугольный участок земли площадью 294 м2 и разделить этот участок забором на две равные части. При каких линейных размерах участка длина всего забора будет наименьшей?
- Сечение оросительного канала имеет форму равнобочной трапеции, боковые стороны которой равны меньшему основанию. При каком угле наклона боковых сторон сечение канала будет иметь наибольшую площадь?
- Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен а. При каких размерах сторон прямоугольника окно будет пропускать наибольшее количество света?
- В точках А и В находятся источники, сила света которых соответственно равна F1 и F2. Расстояние между точками а. На отрезке АВ найти наименее освещенную точку М. (Замечание: Освещенность точки источником света силой F обратно пропорционально квадрату расстояния r ее от источника света:
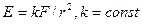 .)
.) - Из круглого бревна, диаметр которого d, требуется вырезать балку прямоугольного поперечного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка оказывала наибольшее сопротивление на изгиб? (Замечание. Сопротивление балки на изгиб пропорционально произведению ширины x ее поперечного сечения на квадрат его высоты y:
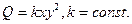 )
)
В задачах найти неопределенные интегралы
- а)
 б)
б) 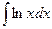 в)
в) 
- а)
 б)
б)  в)
в) 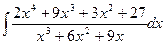
- а )
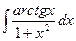 б)
б)  в)
в) 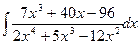
- а)
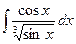
 б)
б) 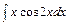 в)
в) 
- а)
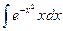 б)
б)  в)
в) 
- а)

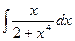 б)
б) 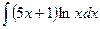 в)
в) 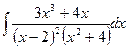
- а)
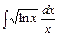
 б)
б) 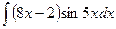 в)
в) 
- а)

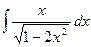 б)
б)  в)
в) 
- а)
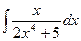 б)
б) 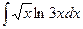 в)
в) 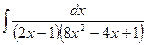
- а)
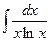
 б)
б)  в)
в) 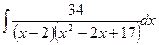
- а)
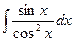
 б)
б) 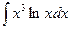 в)
в) 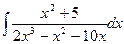
- а)

 б)
б) 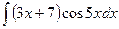 в)
в) 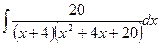
- а)

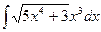 б)
б) 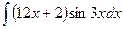 в)
в) 
- а)
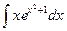 б)
б) 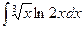 в)
в) 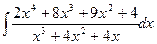
- а)
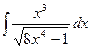
 б)
б) 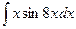 в)
в) 
- а)
 б)
б)  в)
в) 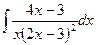
- а)
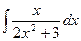 б)
б) 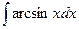 в)
в) 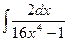
- а)
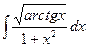
 б)
б)  в)
в) 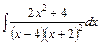
- а)
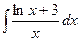
 б)
б) 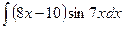 в)
в) 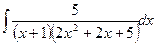
- а)
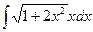
 б)
б) 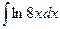 в)
в) 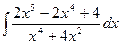
В задачах 261-280.а)Вычислить площади фигур, ограниченных графиками функций; б) вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат.
- а)
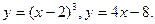 б)
б) 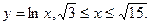
- а)
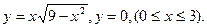 б)
б) 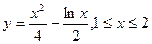
- а)
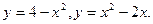 б)
б) 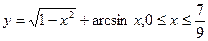
- а)
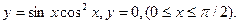 б)
б) 
- а)
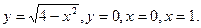 б)
б) 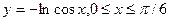
- а)
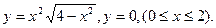 б)
б) 
- а)
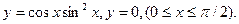 б)
б) 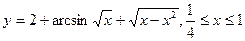
- а)
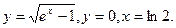 б)
б) 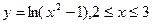
- а)
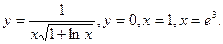 б)
б) 
- а)
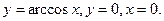 б)
б) 
- а)
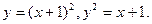 б)
б) 
- а)
 б)
б) 
- а)
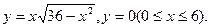 б)
б) 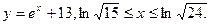
- а)
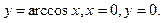 б)
б) 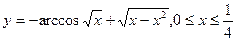
- а)
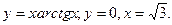 б)
б) 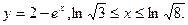
- а)
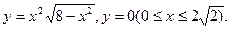 б)
б) 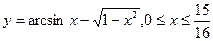
- а)
 б)
б) 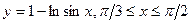
- а)
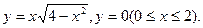 б)
б) 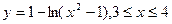
- а)
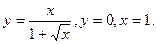 б)
б) 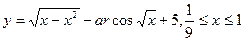
- а)
 б)
б) 
В задачах 281-290 найти общий интеграл дифференциального уравнения. (Ответ представить в виде 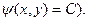
В задачах 291-300 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.
-
 .
. -
 .
. -
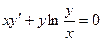 .
. -
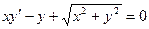 .
. -
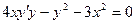 .
. -
 .
. -
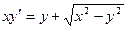 .
. -
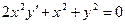 .
. -
 .
. -
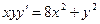 .
.
В задачах 301-310 найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.
-
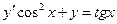 ,
, 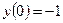 .
. -
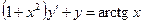 ,
, 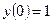 .
. -
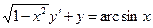 ,
, 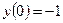 .
. -
 ,
, 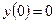 .
. -
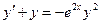 ,
, 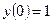 .
. -
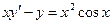 ,
, 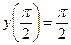 .
. -
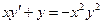 ,
, 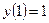 .
. -
 ,
, 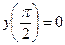 .
. -
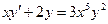 ,
, 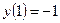 .
. -
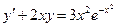 ,
, 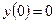 .
.
Дата добавления: 2014-12-05; просмотров: 1386;