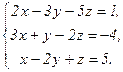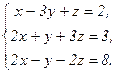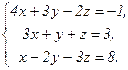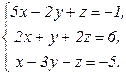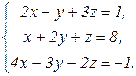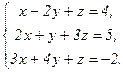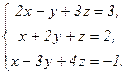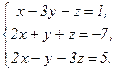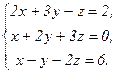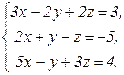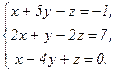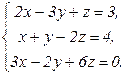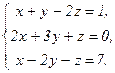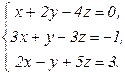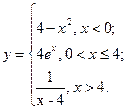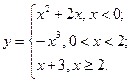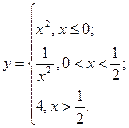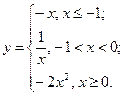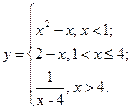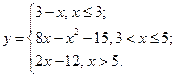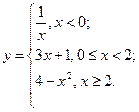Доверительный интервал 1 страница
Статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q-Q*|<d можно лишь говорить о вероятности g, с которой это неравенство осуществляется.
Надежностью (доверительной вероятностью) оценки Q по Q* называют вероятность g, с которой осуществляется неравенство |Q-Q*|<d, то есть
R (|Q-Q*| < d ) = g.
Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к 1 (0,95; 0,99; 0,999). Заменим неравенство |Q-Q*| < d двойным неравенством, равносильным ему:
-d < Q-Q* < d или Q*-d< Q<Q*+ d.
Имеем: R( Q*-d< Q < d+Q*) = g.
Это соотношение означает, что вероятность того, что интервал (Q*-d; Q*+d) заключает в себе (покрывает) неизвестный параметр Q, равна ¡.
Доверительным называют интервал (Q*-d; Q*+d), который покрывает неизвестный параметр с заданной надежностью g.
Метод доверительных интервалов разработан американским статистиком Ю.Нейманом, исходя из идей английского статистика Р.Фитера.
Пример. Из стада коров произведена случайная выборка, получено 20 вариант удоя коров за 300 дней лактации (в ц):
| 35,9 | 35,3 | 42,7 | 45,2 | 25,9 | 35,3 | 33,4 | 27,0 | 35,9 | 38,8 |
| 33,7 | 38,6 | 40,9 | 35,5 | 44,1 | 37,4 | 34,2 | 30,8 | 38,4 | 31,3 |
Требуется: 
1) получить вариационный ряд и построить полигон или гистограмму;
2) вычислить выборочную среднюю, моду, медиану, отклонение, коэффициент вариации, ошибку средней;
3) с надёжностью 95% указать доверительный интервал для оценки генеральной средней.
Решение:
1). Максимальное значение признака составляет 46,2ц, а минимальное – 25,9ц: хmax = 46,2; xmin = 25,9. Разница между ними составляет xmax – xmin = 46,2 – 25,9 = 20,3ц. Этот интервал надо разбить на определенное количество классов. При малом объеме выборки (n<50) намечают 5 – 6 классов, при n>50 – 8 – 9 классов.
Возьмем длину классового интервала Dхi =4: Dхi= 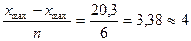 . (округляем до следующего целого числа).
. (округляем до следующего целого числа).
Получаем шесть интервалов: 24 – 28; 28 – 32; 32 – 36; 36 – 40; 40 – 44; 44 – 48 (начало первого класса не обязательно должно совпадать со значением минимальной варианты).
Определим частоту попадания вариант выборки в каждый интервал.
Найдем относительные частоты попадания вариант выборки в каждый интервал:
wi = 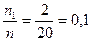 w4 =
w4 = 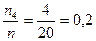
w2 = 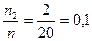 w5 =
w5 = 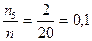
w3 = 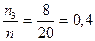 w6 =
w6 = 
Для проверки вычисляем сумму относительных частот:
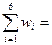 0,1 + 0,1 + 0,4 + 0,2 +0,1 + 0,1 = 1.
0,1 + 0,1 + 0,4 + 0,2 +0,1 + 0,1 = 1.
Тот факт, что в сумме получили единицу, подтверждает правильность вычислений.
По формуле 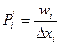 вычислим плотность
вычислим плотность 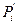 относительных частот вариант. Получаем:
относительных частот вариант. Получаем:
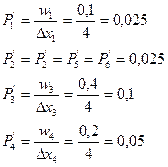
Расположим результаты выборки в таблице:
| Интервал значений удоя(ц) | 24-28 | 28-32 | 32-36 | 36-40 | 40-44 | 44-48 |
| Частота варианты ni | ||||||
| Относительная частота wi | 0,1 | 0,1 | 0,4 | 0,2 | 0,1 | 0,1 |
| Плотность относительной частоты pi | 0,025 | 0,025 | 0,1 | 0,05 | 0,025 | 0,025 |
Строим гистограмму относительных частот – ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются классовые интервалы, а высотами – соответствующие значения плотностей относительных частот 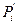 . Классовые интервалы
. Классовые интервалы
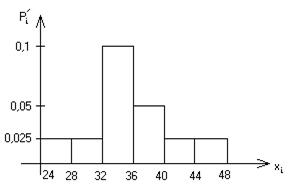
изображают на оси абсцисс, а значения 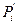 откладывают на оси ординат.
откладывают на оси ординат.
2). Основные выборочные характеристики вычисляются по формулам:
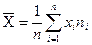 - выборочная средняя;
- выборочная средняя;
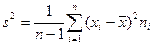 - дисперсия;
- дисперсия;
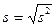 - среднее квадратическое отклонение;
- среднее квадратическое отклонение;
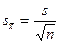 - ошибка средней;
- ошибка средней;
 % - коэффициент вариации.
% - коэффициент вариации.
Расчеты  и s2 удобно проводить с помощью таблицы.
и s2 удобно проводить с помощью таблицы.
| № п/п | Интервал значений удоя (ц) | Серединное значение интервала xi | Частота варианты ni | xini | xi- 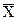
| (xi- 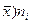
|
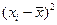
| 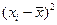 ni ni
|
| 24-28 | -9,6 | -19,2 | 92,16 | 184,32 | ||||
| 28-32 | -5,6 | -11,2 | 31,36 | 62,72 | ||||
| 32-36 | -1,6 | -12,8 | 2,56 | 20,48 | ||||
| 36-40 | 2,4 | 9,6 | 5,76 | 23,04 | ||||
| 40-44 | 6,4 | 12,8 | 40,96 | 81,92 | ||||
| 44-48 | 10,4 | 20,8 | 108,16 | 216,32 | ||||
| 588,8 |
 = 35,6, М0 = 34 – значение варианты, имеющей наибольшую частоту; Ме = 36 – значение варианты, лежащей в середине ряда.
= 35,6, М0 = 34 – значение варианты, имеющей наибольшую частоту; Ме = 36 – значение варианты, лежащей в середине ряда.
s2 =  ; s = 5,57;
; s = 5,57; 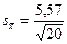 = 1,25.
= 1,25.
V = 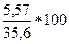 % = 15,6%/
% = 15,6%/
Поскольку 10% < V < 20%, то изменчивость удоев за 300 дней следует считать средней.
3). Доверительный интервал для оценки генеральной средней определяется как
 ,
,
где величина 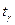 при заданной надежности определяется с помощью таблиц приложения 1. В нашем примере
при заданной надежности определяется с помощью таблиц приложения 1. В нашем примере
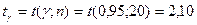
Вычисляем радиус доверительного интервала:
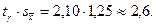
Получаем:
35,6 – 2,6 < 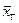
 < 35,6 + 2,6
< 35,6 + 2,6
33 < 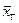 < 38,2.
< 38,2.
Таким образом, с надежностью 95% можно утверждать, что во всем стаде средний удой за 300 дней (генеральная средняя) заключен в пределах от 33ц (гарантированный минимум) до 38,2ц (возможный максимум).
Вопросы для самопроверки
1.Поясните на примерах понятия генеральной совокупности и выборки.
2.Приведите примеры варьирующих признаков (случайных величин) и вариант выборки.
3.Что такое вариационный ряд распределения? Как определяется относительная частота варианты?
4.Как строится гистограмма относительных частот распределения? Чему равна её площадь?
5.Перечислите основные выборочные характеристики. Как они вычисляются?
6.Что характеризуют дисперсия и среднее квадратическое отклонения?
7.Для каких целей используется коэффициент вариации?
8.Что характеризует ошибка средней?
9.Что понимают под доверительным интервалом для оценки генеральной средней? Как найти доверительный интервал при заданной надёжности (доверительной вероятности)?
10.Как изменится величина доверительного интервала, если увеличить надёжность?
11.Что понимают под представительностью (репрезентативностью) выборки? Как достигается представительность выборки при отборе?
12.Как вычислить выборочную среднюю и дисперсию в случае сгруппированных данных?
Задачи для контрольных работ
В задачах 1-20 даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) Внутренний угол В в радианах с точностью до 0,01; 4) уравнение медианы АЕ; 5) уравнение и длину высоты СD; 6) уравнение прямой, проходящей через точку Е параллельно стороне АВ и точку М ее пересечения с высотой СD.
- А(1; -1), В(4; 3), C(5; 1).
- А(0; -1), В(3; 3), C(4; 1).
- А(1; -2), В(4; 2), C(5; 0).
- А(2; - 2), В(5; 2), C(6; 0).
- А(0; 0), В(3; 4), С(4; 2).
- А(0; 1), В(3; 5), C(4; 3).
- А(3;-2), В(6; 2), С(7; 0).
- А(3;-3), В(6; 1), С(7;-1).
- А(-1; 1), В(2; 5), С(3; 3).
- А(4; 0), В(7; 4), С(8; 2).
- А(2; 2), В(5; 6), С(6; 4).
- А(4; -2), В(7; 2), С(8; 0).
- А(0; 2), В(3;6),С(4;4).
- А(4; 1), В(7; 5), С(8; 3).
- А(3; 2), В(6; 6), С(7; 4).
- А(-2; 1), В(1; 5), С(2; 3).
- А(4; -3), В(7; 1), С(8; -1).
- А(-2; 2), В(1; 6), С(2; 4).
- А(5; 0), В(8; 4), С(9; 2).
- А(2; 3), В(5; 7), С(6; 5).
В задачах 21-40 решить систему трех уравнений с тремя неизвестными по формулам Крамера
В задачах 41-60 найти указанные пределы.
- а)
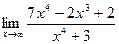 ; б)
; б) 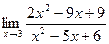 .
. - а)
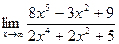 ; б)
; б) 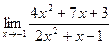 .
. - а)
 ; б)
; б) 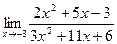 .
. - а)
 ; б)
; б) 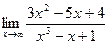 .
. - а)
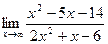 ; б)
; б) 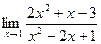 .
. - а)
 ; б)
; б) 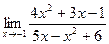 .
. - а)
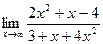 ; б)
; б)  .
. - а)
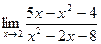 ; б)
; б)  .
. - а)
 ; б)
; б) 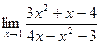 .
. - а)
 ; б)
; б)  .
. - а)
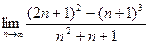 ; б)
; б) 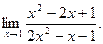
- а)
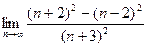 ; б)
; б) 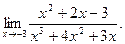
- а)
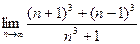 ; б)
; б) 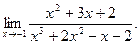
- а)
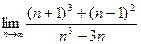 ; б)
; б) 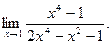
- а)
 ; б)
; б) 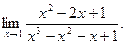
- а)
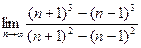 ; б)
; б) 
- а)
 ; б)
; б) 
- а)
 ; б)
; б) 
- а)
 ; б)
; б) 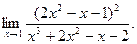
- а)
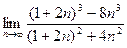 ; б)
; б) 
В задачах 61-80 найти указанные пределы.
- а)
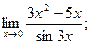 б)
б) 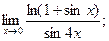 в)
в) 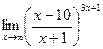 .
. - а)
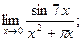 б)
б)  в)
в)  .
. - а)
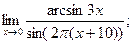 б)
б) 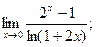 в)
в) 
- а)
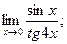 б)
б)  в)
в) 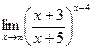 .
. - а)
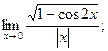 б)
б) 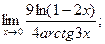 в)
в) 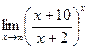 .
. - а)
 б)
б) 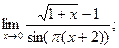 в)
в) 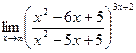 .
. - а)
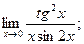 б)
б) 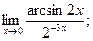 в)
в) 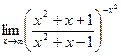 .
. - а)
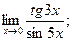 б)
б) 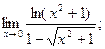 в)
в) 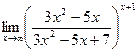 .
. - а)
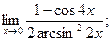 б)
б)  в)
в) 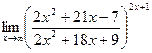 .
. - а)
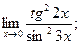 б)
б) 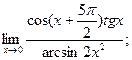 в)
в)  .
. - а)
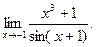 б)
б)  в)
в) 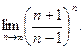
- а)
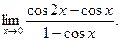 б)
б)  в)
в) 
- а)
 б)
б) 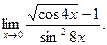 в)
в) 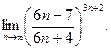
- а)
 б)
б)  в)
в) 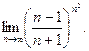
- а)
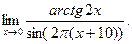 б)
б) 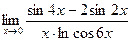 в)
в) 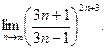
- а)
 б)
б) 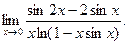 в)
в) 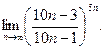
- а)
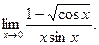 б)
б) 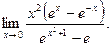 в)
в) 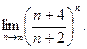
- а)
 б)
б) 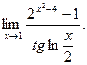 в)
в) 
- а)
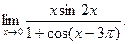 б)
б) 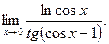 в)
в) 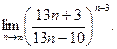
- а)
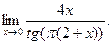 б)
б) 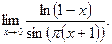 в)
в) 
В задачах 81-90 даны функция 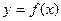 . Требуется: 1) исследовать функцию на непрерывность; 2) установить тип точек разрыва; 3) построить график функции в окрестности точек разрыва.
. Требуется: 1) исследовать функцию на непрерывность; 2) установить тип точек разрыва; 3) построить график функции в окрестности точек разрыва.
-
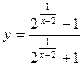
-
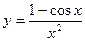
-
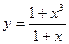
-
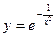
-
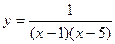
-
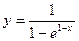
-
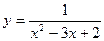
-
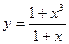
-
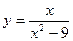 .
. -
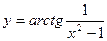 .
.
В задачах 91-100 функция 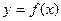 задана различными аналитическими выражениями для различных областей изменения аргумента
задана различными аналитическими выражениями для различных областей изменения аргумента 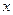 . Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти односторонние пределы и скачок функции в точках разрыва; 3) построить график функции в окрестности точек разрыва.
. Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти односторонние пределы и скачок функции в точках разрыва; 3) построить график функции в окрестности точек разрыва.
В задачах 101-120 найти производные 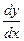 , пользуясь формулами дифференцирования.
, пользуясь формулами дифференцирования.
- а)
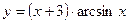 ; б)
; б) 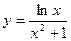 ; в)
; в) 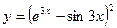 .
. - а)
 ; б)
; б) 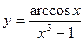 ; в)
; в) 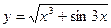 .
. - а)
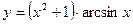 ; б)
; б) 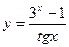 ; в)
; в) 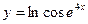 .
. - а)
 ; б)
; б) 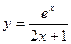 ; в)
; в) 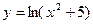 .
. - а)
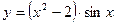 ; б)
; б) 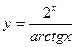 ; в)
; в)  .
. - а)
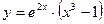 ; б)
; б)  ; в)
; в) 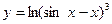 .
. - а)
 ; б)
; б) 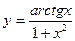 ; в)
; в) 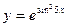 .
. - а)
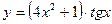 ; б)
; б)  ; в)
; в)  .
. - а)
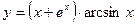 ; б)
; б) 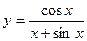 ; в)
; в)  .
. - а)
 ; б)
; б)  ; в)
; в) 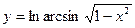 .
. - а)
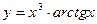 ; б)
; б)  ; в)
; в) 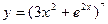 .
. - а)
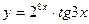 ; б)
; б) 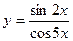 ; в)
; в) 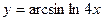 .
. - а)
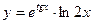 ; б)
; б) 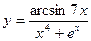 ; в)
; в) 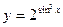 .
. - а)
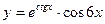 ; б)
; б) 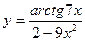 ; в)
; в) 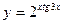 .
. - а)
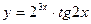 ; б)
; б) 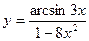 ; в)
; в) 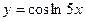 .
. - а)
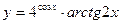 ; б)
; б) 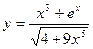 ; в)
; в)  .
. - а)
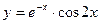 ; б)
; б) 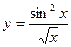 ; в)
; в) 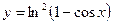 .
. - а)
 ; б)
; б)  ; в)
; в) 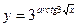 .
. - а)
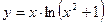 ; б)
; б)  ; в)
; в) 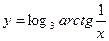 .
. - а)
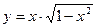 ; б)
; б) 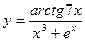 ; в)
; в) 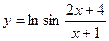 .
.
Дата добавления: 2014-12-05; просмотров: 1817;