Статистические оценки параметров распределения

Пусть требуется изучить количественный признак генеральной совокупности. Пусть удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение.

Например, если известно, что изучаемый признак распределен в генеральной совокупности нормально, то требуется оценить, то есть приближенно найти математическое ожидание (а) и среднее квадратическое отклонение (δ), так как эти два параметра полностью задают нормальное распределение. Если же известно, что признак имеет распределение Пуассона, то необходимо оценить параметр “l”, которым оно определяется.

Обычно оцениваемый параметр выражают через данные выборки, например, через значения количественного признака х₁, х₂,…,х_n, полученные в результате наблюдений.

Статистической оценкой неизвестного параметра теоретического распределения называют его приближенное значение, зависящее от данных выборки (х₁, х₂,…, х_k; n₁, n₂ ,…,n_k), то есть некоторую функцию этих величин.

x₁, х₂, …,х_k - значения признака; n₁, n₂, …, n_k - частоты. Статистическая оценка является случайной величиной.

Пусть Θ – оцениваемый параметр, Θ* - его статистическая оценка. Ясно, что Θ* тем точнее определяет параметр Θ, чем меньше абсолютная величина разности |Θ - Θ*|. Другими словами, если δ >0 и |Θ - Θ*|< δ, то чем меньше δ, тем оценка точнее. Таким образом, величину |Θ - Θ*| называют точностью оценки, а число δ характеризует точность оценки.

Чтобы оценка Θ* имела практическое значение, она не должна содержать систематической ошибки и вместе с тем иметь возможно меньшую дисперсию. При этом если оценка Θ* дает приближенное значение Θ с избытком (Θ* > Θ), то и математическое ожидание (среднее значение) M(Θ*)>Θ; если же Θ* дает оценку с недостатком (Θ* < Θ), то и M (Θ*) < Θ. На основании этого делаем вывод, что соблюдение требований M(Θ*) = Θ гарантирует от получения систематических ошибок.

Оценка параметра называется несмещенной, если ее математическое ожидание M (Θ*) равно оцениваемому параметру Θ, то есть M (Θ*) = Θ и смещенной, если M(Θ*) ¹ Θ.

Оценка Θ* называется эффективной, если при заданном объеме выборки “n” она имеет наименьшую дисперсию.

Оценка Θ* называется состоятельной, если при любом δ > 0:

lim P (|Θ - Θ*|< δ) = 1, то есть оценка Θ* сходится по вероятности к Θ.

Теорема1. Выборочная средняя 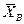является несмещенной и состоятельной оценкой математического ожидания.

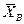является и эффективной оценкой M (Х).

Теорема 2. Исправленная выборочная дисперсия 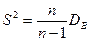является несмещенной и состоятельной оценкой дисперсии D(Х).