Модели расчетных схем курсовой стоимости обыкновенных акций

Как отмечалось выше, предсказать цену акции с помощью формулы (16.31) нельзя, но можно установить ориентировочный уровень курса, вокруг которого теоретически цена должна изменяться.

Так как дивиденды образуют финансовую ренту, и, поскольку акция является бессрочной ценной бумагой (считаем n =>∞), то формула определения курсовой стоимости (современной стоимости финансовой ренты) примет вид:

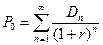, (16.33)

где Р_о – цена акции, D_п – ожидаемый годовой платеж (дивиденд) в году п, r – ставка дисконтирования (доходности) по альтернативному вложению с таким же уровнем риска, как и риск вложения в данные акции.

Если положить, что ожидаемые годовые дивиденды равны, то формула (16.33) имеет вид:

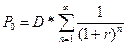(16.34)

где

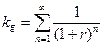
– коэффициент дисконтирования финансовой ренты. При выводе формулы пожизненной ренты мы показали, что k_g = 1/r при п =>∞. Отсюда следует, что цена акции может быть определена практически по формуле:

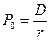(16.35)

Если ожидается, что дивиденды предприятия будут расти постоянными темпами, то формула (16.33) примет вид:

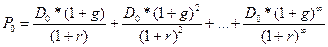, (16.36)

где D₀ – дивиденды в расчете на одну акцию в настоящий момент; g – темп прироста дивиденда, и при этом он постоянен, r –приемлемая ставка дисконтирования.

Предположим, что r > g, то уравнение (16.36) можно представить, как:

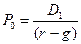(16.37)

где D₁ – ожидаемый дивиденд на следующий период.

Формула (16.33) несколько видоизменится, если инвестор планирует владеть акцией некоторое время, а затем продать Данный стиль поведения инвестора является наиболее характерным на рынке и связан с деловым циклом акционерного общества. Если вкладчик приобретает акцию молодой компании, то он рассчитывает на ее активный рост, связанный с открытием рынков новой продукции или завоеванием уже существующих рынков с помощью новых технологий. Данный период роста акционерного общества в случае успеха связан с высокими доходами. Однако через некоторое время акционерное общество вступает в период зрелости, когда темп роста доходов сокращается вследствие насыщения рынка его продукцией. В этом случае акцию целесообразно продать. Аналогичные рассуждения относятся и к уже зрелым компаниям. Таким образом, если инвестор планирует в будущем продать акцию, то он может оценить ее стоимость по формуле:

, (16.38)

где Р_n – цена акции в конце n-го периода, когда инвестор планирует продать ее.

В данной формуле, как и в первой, сложность возникает как с прогнозированием дивидендов, так и с прогнозированием цены будущей продажи акции.

Простейшая модель прогнозирования дивидендов предполагает, что они будут расти с постоянным темпом. Тогда дивиденд для любого года можно рассчитать по формуле:

, (16.39)

где D₀ – дивиденд текущий (известный); D_t – расчетный дивиденд; g – известный темп прироста дивиденда.

Темп прироста дивиденда определяется на основе данных по выплате дивидендов за предыдущие годы.

Для простых акций вместо ежегодного дивиденда можно использовать данные по ожидаемой прибыли в расчете на одну акцию и ее темпа прироста, тогда цену акции можно определить по следующей формуле:

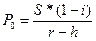, (16.40)

где S – ожидаемая прибыль в расчете на одну акцию; i – ставка капитализации чистой прибыли; r – ставка дисконтирования; h –темп ежегодного прироста прибыли акционерного общества.

В случае если акционерное общество не выплачивает дивидендов, то этот процесс завершится с вступлением его в фазу зрелости, когда окончится его экстенсивный рост. После этого оно начнет выплачивать дивиденды. В этом случае курсовая стоимость акции будет определяться по следующей формуле:

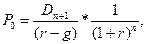(16.41)

где D_n+1 – первый дивиденд, который выплатит акционерное общество инвестору в (n+1) – году, r – ставка дисконтирования; g – темп прироста дивиденда.

Отметим, что ориентировочная цена акции может устанавливаться на основе привлечения бухгалтерского учета и использоваться для оценки акций на первичном рынке ценных бумаг и реальности цены предложения на вторичном рынке.