Моделирование расчетных показателей купонной облигации с периодической выплатой процентов и их реинвестированием

Операции с этим видом облигаций осуществляются в основном с частными лицами. Доход в этом случае будет состоять из купонного дохода D_k и разницы между номиналом N и ценой покупки Р:

(16.17)

Используя выражение (16.2), имеем:

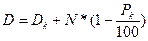, (16.18)

где Р_к – курс купонной облигации.

Будем считать, что проценты, получаемые в течение срока облигации, реинвестируются. В этом случае значение D_kбудет определяться как наращенная сумма постоянной ренты постнумерандо, размер платежа которой равен:

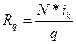(16.19)

где q – количество выплат купонных процентов по облигации в течение года; i_k – купонный процент.

Если купонные выплаты по облигации в течение п лет осуществляются q раз в год и получаемые купонные проценты вновь инвестируются по ставке i_p с начислением на них процентов m раз в год (m/q), то значение D_k в соответствии с формулой (16.19) будет равно:

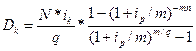(16.20)

Следовательно, общий доход инвестора составит:

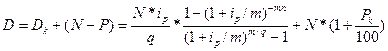(16.21)

Для определения курсовой стоимости данной облигации используем общий принцип ее расчета, описанный выше: определим дисконтированную стоимость номинала, дисконтированную стоимость величины будущих купонных доходов и полученные значения просуммируем.

Данная сумма и будет представлять курсовую стоимость купонной облигации.

Пусть i_k, i_{p –}ставка купона и ставка реинвестирования (дисконтирования) процентных денег, которая соответствует уровню риска, установившемуся на рынке ценных бумаг. Если облигация номиналом N куплена за п лет до ее погашения, купонные выплаты осуществляются q раз в год и полученные купонные проценты вновь инвестируются т раз в год по номинальной процентной ставке i_p, то размер платежа (будущие купонные доходы), определяемые формулой (16.19), есть годовая финансовая рента.

Тогда дисконтированная стоимость номинала будет определяться формулой:

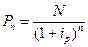(16.22)

Дисконтированная стоимость финансовой ренты в соответствии с формулами (16.19) и (16.20) составит:

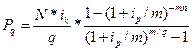(16.23)

Следовательно, курсовая стоимость такой облигации будет определяться выражением:

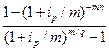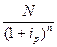+ (16.24)

а курс облигации такого вида будет равен:

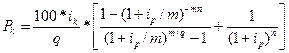(16.25)

Положив в формулу (16.25) m = n = q = 1, имеем:

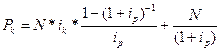(16.26)

Поскольку дисконтированная стоимость ренты больше нуля, из приведенной формулы (16.26) можно сразу же сделать следующие выводы:

1. Если купонная ставка i_k равна текущей процентной ставке i_p, то курсовая стоимость равна номинальной стоимости облигации.

2. Если купонная ставка i_k меньше текущей процентной ставки i_p (i_k< i_p), то курсовая стоимость меньше номинальной. В этом случае говорят, что облигация куплена с дисконтом. Поскольку при низкой купонной ставке для инвесторов предпочтительнее вложение средств в более доходные финансовые инструменты, то продажа облигации по цене ниже номинала дает возможность получения дополнительного дохода.

3. Если купонная ставка выше i_kноминальной процентной ставки i_p (i_k >i_p), то курсовая стоимость выше номинальной (курс выше 100). В этом случае облигация продается с премией. Поскольку купонная ставка выше текущей процентной ставки, то для уравнивания доходности с рыночной курсовая стоимость должна быть выше номинальной на величину премии, которая уменьшает доходность операции до i_p.

Оценка облигации производится не только в момент эмиссии, но и в любой момент времени вплоть до момента погашения. В любой момент времени облигация может быть продана или приобретена на рынке ценных бумаг по рыночной цене.

Теперь определим доходность облигации рассматриваемого типа, используя эффективную ставку сложных процентов j_эс..

Пусть инвестор купил купонную облигацию номиналом N с периодической выплатой процентов qраз в год по курсовой стоимости Рсо сроком погашения через п лет. При этом полученные купонные проценты вновь инвестируются т раз в год.

Для определения эффективной ставки сложных процентов j_эс вначале рассчитаем дохода, получаемый от покупки такой облигации по следующей формуле:

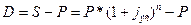(16.27)

Отсюда выводим j_эс

(16.28)

Используя формулы (16.17) и (16.18), имеем:

(16.29)

где купонный доход D_к может быть рассчитан по формуле (16.20). Отметим, что между курсовой стоимостью Р и ее доходностью j_эс до погашения облигации существуют следующие зависимости:

1. Цена облигации и доходность до погашения находятся в обратной связи. При повышении доходности цена облигации падает, при понижении – возрастает.

2. Если доходность до погашения выше купонного процента, облигация продается со скидкой.

3. Если доходность до погашения ниже купонного процента, облигация продается с премией.

4. Если доходность до погашения равна купонному проценту, цена облигации равна номиналу.

5. При понижении доходности до погашения на 1%, цена облигации возрастает в большей степени в сравнении с ее падением при увеличении доходности до погашения на 1%.