Доход, курсовая стоимость и доходность бескупонной облигации

Облигация такого вида обеспечивает доход за счет разницы между номинальной стоимостью облигации и ее рыночной ценой (дисконтный доход). Формализуем данное высказывание. Так, если облигация имеет номинальную стоимость N, а покупная цена (рыночная) составляет Р, тогда доход от облигации составит:

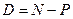(16.3)

Используя формулу (16.2.), выражение (16.3) примет вид:

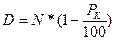(16.4)

Доход здесь рассматривается в денежном выражении, который и образует дисконтный доход такой облигации.

Перейдем непосредственно к рассмотрению курсовой стоимости такой облигации.

Прежде всего, отметим, что определение курсовой стоимости любой ценной бумаги основано на принципе дисконтирования. Инвестор приобретает ценную бумагу, чтобы получать доходы, которые она приносит. Поэтому для ответа на вопрос, сколько сегодня должна стоить та или иная ценная бумага, необходимо определить дисконтированную стоимость всех доходов, которые она приносит.

Общий принцип расчета курсовой стоимости состоит из трех действий: 1) определяем поток доходов, которые ожидаются по данной бумаге; 2) находим дисконтированную (современную) стоимость величины каждого платежа по ценной бумаге; 3) суммируем дисконтированные стоимости. Данная сумма и представляет собой курсовую стоимость ценной бумаги.

Так как мы имеем бескупонную облигацию, т.е. текущих выплат нет, то современная стоимость потока доходов нулевая.

Достаточно найти современную стоимость номинала, которая и будет определять курсовую стоимость облигации на момент оценки.

Пусть облигация куплена за плет до погашения. Дисконтируем номинальную стоимость облигации N по годовой сложной процентной ставке j, которая принимает значения доходности альтернативного вложения денежных средств с таким же сроком и риском, размер доходности которой определяется на рынке ценных бумаг.

Курсовая стоимость такой облигации составит:

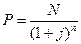(16.5)

Это есть максимальная цена, по которой целесообразно покупать данную облигацию. Тогда, в соответствии с (16.2), курс облигации на момент ее оценки составит:

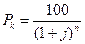(16.6)

Становится понятным, что для такой облигации курс всегда меньше 100. Как правило, облигации такого вида имеют короткий срок погашения (до года).

Государственные краткосрочные облигации (ГКО) имеют срок погашения от 3 до 12 месяцев. В этом случае курсовая стоимость ГКО будет определяться по формуле:

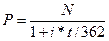, (16.7)

где Р – курсовая стоимость ГКО; N – номинал ГКО; i – доходность ГКО; t – количество дней от момента покупки до погашения ГКО.

Доход и курсовая стоимость бескупонной облигации рассматриваются в денежном выражении.

Сравнивая доходность от различных операций на финансовом рынке, можно определить, в какой финансовый инструмент выгоднее вложить деньги.

Определим доходность от покупки бескупонной облигации, используя эффективную ставку простых процентов

Если инвестор вложил денежные средства в размере Р на покупку облигаций в некоторый банк под простую эффективную процентную ставку i_эп на срок погашения (t/к), то наращенная сумма Sпримет значение:

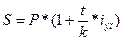, (16.8)

где t – интервал времени, за который гасится облигация;

k – размер финансового года (360 дней) (исключение составляют ГКО и другие государственные займы, где k =365 дней).

Используя формулу 16.2, имеем:

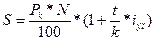(16.9)

Тогда доход от покупки такой облигации составит:

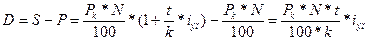(16.10)

Сопоставив выражения (16.4) и (16.10), имеем:

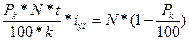(16.11)

Отсюда, сделав ряд преобразований, получим:

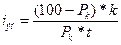(16.12)

Если для измерения доходности использовать эффективную ставку сложных процентов j_эс то величина наращенной суммы S примет вид:

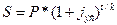(16.13)

Тогда доход от покупки такой облигации составит:

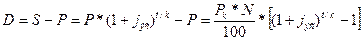(16.14)

Сопоставив выражения (16.4) и (16.14), имеем:

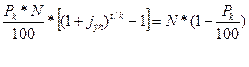(16.15)

Отсюда, сделав некоторые преобразования, получим:

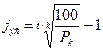(16.16)

Если сопоставить результаты расчетов доходности облигации по ставкам простых и сложных процентов, можно, увидеть, что доходность облигации несколько выше, если проводить расчеты по эффективной ставке простых процентов.