Тема 11. Практический маркетинг
11.1. Функция рыночного спроса
Функцией спроса называется зависимость величины спроса от влияющих факторов в течение определенного периода времени. Функция спроса может быть представлена в виде следующего равенства:
Q = q(Ц, Цд, Цз, Дп, Вп, Оп), (11.1)
где:
Q – величина спроса на товар;
Ц – цена товара;
Цд – цена товаров, дополняющих данный товар в потреблении;
Цз – цены товаров, заменяющих данный товар в потреблении;
Дп – доход потребителей товара;
Вп - вкусы потребителей;
Оп – ожидания потребителей.
Все факторы, кроме цены данного товара, называются неценовыми. Очевидно, что одновременное рассмотрение всех факторов, влияющих на величину спроса, затруднительно. Допустим, что неценовые факторы спроса на рассматриваемом периоде времени не меняются.
Зависимость величины рыночного спроса от цены данного товара называется функцией спроса от цены при прочих равных условиях.
Между ценой данного товара Ц и величиной спроса на него Q существует обратная зависимость: чем выше цена, тем меньше величина спроса и наоборот, чем меньше цена, тем больше величина спроса. Зависимость между ценой спроса и величиной спроса, называется законом спроса. Он подтверждается на практике. Изменение цены приводит к изменению величины спроса, что означает движение вдоль кривой спроса.
Если функция спроса имеет линейный характер, то
Q = a – b * Ц, (11.2)
где: а и b – постоянные коэффициенты.
Коэффициенты а и b определяются путем продолжения линии спроса до пересечения с координатными осями.
Наклон кривой спроса для любых значений цены и величины спроса будет: dQ /dЦ= - b, т.е. постоянен и отрицателен. (см.рис.11.1).Отрицательный знак показывает, что с увеличением величины Ц спрос Q будет уменьшаться и наоборот.
 Ц
Ц
Q = a – b* Ц

 a/ b
a/ b

 Ц1 Е
Ц1 Е

 0 Q1 а Q
0 Q1 а Q
Рис. 11.1. Линейная функция спроса
Для нелинейной функции спроса наклон кривой спроса будет изменяться при изменении цены. Так, если
Q = А*Ц –э (11.3)
где «А» и «Э» - постоянные коэффициенты, то используя ранее рассмотренную функцию (8.1) получим для коэффициента «А» следующее выражение:
А = Q1 * Ц1э
Наклон этой кривой спроса равен dQ/dЦ = - А* э* Ц-(э+1), т.е. он отрицателен и зависит от цены (См. рис. 11.2). Отрицательный знак отражает характер зависимости (11.3): с увеличением цены величина спроса будет уменьшаться.

 Ц
Ц
D1
Q = А*Ц -э

 Ц1 Е
Ц1 Е
 0 Q1 Q
0 Q1 Q
Рис. 11.2. Нелинейная функция спроса
Воздействие неценовых факторов приводит к изменению спроса на товар. В этом случае кривая спроса D1 сдвигается вправо, если эти факторы вызывают увеличение спроса D2, и влево, если факторы вызывают уменьшение спроса D3 (cм. рис. 11.3).
 Ц
Ц
 D2 D2 > D1> D3
D2 D2 > D1> D3

 D1
D1
 D3
D3

Q
Рис.11.3.Сдвиг рыночного спроса вследствие влияния неценовых факторов
Рассмотрим смысл понятия эластичности «э». При исследовании рынков возникает необходимость связать изменения цены и объёма спроса в одном показателе. Использование для этой цели абсолютных величин неприемлемо, так как цены измеряются в денежных единицах, а объём спроса в натуральных величинах. Поэтому речь может идти только об относительных изменениях цен и объемов, не зависящих от единиц измерения. Таким показателем является эластичность, характеризующая меру реагирования относительного изменения одной переменной величины на относительное изменение другой переменной величины. Величина эластичности спроса по цене показывает процентное изменение спроса на товар в результате изменения его цены на один процент.
Покажем это с помощью формулы (11.3):
Q = А * Ц-э = Q1 * Ц1э * Ц-э
Выполним следующие преобразования:
Q / Q1 = (Ц1 / Ц)э, далее применяя процедуру логарифмирования получим:
lnQ – lnQ1 = э * (lnЦ1 – lnЦ) и после дифференцирования:
dQ /Q = - э * dЦ /Ц. Таким образом:
э = │dQ /Q│ : │dЦ /Ц│ (11.4)
Для дискретной функции спроса эластичность спроса по цене определяется по формуле:
э = │∆Q/Q│ : │∆Ц/Ц│ (11.5)
где: Э – эластичность спроса по цене,
∆Q – изменение величины спроса на участке кривой спроса,
∆Ц – изменение цены на этом участке кривой спроса.
Иллюстрируем применение формулы (11.5) для участка кривой спроса между точками с координатами (Q1, Ц1) и (Q2, Ц2). В результате получим:
э = (Q2 – Q1) / (Q2 + Q1)/2 : (Ц2 – Ц1) / (Ц2 + Ц1)/2 (11.6)
В данном случае определяется средняя величина эластичности на рассматриваемом участке кривой спроса.
Анализируя возможные варианты изменения показателей в формуле (11.6) можно установить границы изменения эластичности
∞ ≥ э ≥ 0
Рассмотрим изменение эластичности при движении по линейной функции спроса. С этой целью воспользуемся формулой (11.4) в следующем виде:
э = │dQ /Q│ : │dЦ /Ц│=│dQ/dЦ│ * │Ц / Q│
Как было показано выше для линейной функции спроса Q = а – b * Ц наклон dQ/dЦ не зависит от цены и величины спроса, он равен dQ/dЦ = - b . Напротив, с изменением цены отношение Ц/Q, равное тангенсу угла α, будет меняться (см. рис. 11.4, позиции 1,2,3).
 Ц
Ц
 Эластичный спрос
Эластичный спрос
 Э = ∞
Э = ∞


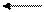
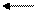
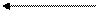

 а/b 3 Э = 1 Неэластичный спрос
а/b 3 Э = 1 Неэластичный спрос



 а/2b 2 1
а/2b 2 1




 Ц Ц Ц Э = 0
Ц Ц Ц Э = 0
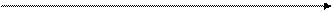 Q α Q=а/2 Q а Q
Q α Q=а/2 Q а Q
Рис.11.4. Изменение эластичности спроса по цене
Таким образом, для линейной функции спроса эластичность спроса по цене является переменной величиной. Определим диапазон её изменения (см. рис.11.4):
- если Q = а, то Ц = 0, следовательно Э = 0;
- если Ц = а/b, то Q = 0, следовательно Э = ∞;
- если Q = а/2, то Ц = а/2b, следовательно Э = │dQ/dЦ │* Ц/Q =
b * (а/2b : а/2) = 1 .
Таким образом, точка единичной эластичности спроса по цене находится в середине линии спроса. Спрос является:
· неэластичным при 1 < Э ≤ 0,
· эластичным при ∞< Э < 1,
Эластичность спроса по цене зависит от наличия товаров, которые могут заменить данный товар в потреблении. Чем больше заменителей имеет данный товар, тем эластичнее спрос по цене на этот товар. Например, к таким товарам относятся автомобили, дорогая мебель.
Эластичность спроса по цене зависит от степени агрегирования товаров. Чем более агрегирована группа товаров, тем меньше у нее заменителей, тем неэластичнее спрос. Например, такой спрос наблюдается в случае приобретения товаров первой необходимости: продуты питания, одежда.
Обычно в долгосрочном периоде спрос на один и тот же товар более эластичен, чем в краткосрочном периоде.
Общая выручка «В» от продажи товара равна произведению цены на количество проданного товара:
В = Ц * Q (11.7)
На графиках линейной и нелинейной функций спроса величина выручки равна площади прямоугольника Ц1ЕQ1O под кривыми спроса (см.рис.11.2 и 11.3).
С учётом (11.2) для линейной функции спроса получим:
В = Ц * (a – b Ц), (11.8)
Анализ функции (11.8) показывает, что выручка В имеет максимум при Ц= а/2b и Q = а/2 (см.рис.11.5).
В

 Эластичный спрос
Эластичный спрос





 а2/4b Неэластичный спрос
а2/4b Неэластичный спрос

 1 1
1 1
2 2
0 а/2 а/b Q
Рис.11.5. Определение максимума выручки в случае линейной функции спроса.
Максимальное значение выручки будет:
Вmax = а/2b *а/2 = а2/4b (11.7)
Таким образом, при снижении цены товара (вариант 1-1) общая выручка продавцов возрастает от «О» до максимального значения на участке эластичного спроса, а затем она снижается от максимального значения до «О» на участке неэластичного спроса. Наоборот, при повышении цены товара (вариант 2-2) общая выручка продавцов возрастает от «О» до максимального значения на участке неэластичного спроса, а затем снижается от максимального значения до «О» на участке эластичного спроса (см. рис.11.4).
Рассмотрим теперь нелинейную функцию спроса (11.3):
Q = A*Ц-э
Как видно, для данной функции спроса эластичность спроса по цене постоянна и равна абсолютному значению показателя степени, т.е. «э». При э=1 такая функция представляет собой гиперболу. В данной модели предполагается, что величина «Э» для всей кривой спроса является постоянной величиной.
Общая выручка продавцов в функции цены будет составлять:
В = Q* Ц = А* Ц1-э =Q1* Ц1 э *Ц1-э (11.8)
Общая выручка продавцов в функции величины спроса будет составлять
В = Ц * Q = Ц1* Q11/э * Q 1-1/э (11.9)
Из анализа формулы (11.9) следует, что характер функции В(Q) в зависимости от величины показателя «Э» будет изменяться. На следующем графике показана функция В(Q) для различных значений показателя «Э»:
Выручка «В» 
 Э>1
Э>1
Э< 1
Э=1 
 Q
Q
Рис.11.6. Изменение выручки при разных величинах показателя эластичности «Э»
При величине э=1 общая выручка продавцов будет постоянна и равна:
В = Ц*Q = Ц * A*Ц-1 = А = Q1* Ц1 (11.10)
Таким образом, когда функция спроса представляет собой гиперболу, выручка продавцов не зависит от величины спроса Q.
При эластичном спросе (Э > 1) выручка, как видно из графика, будет расти с увеличением объема выпускаемой продукции.
При неэластичном спросе (Э < 1) выручка будет уменьшаться с увеличением объема выпускаемой продукции.
Эти положения следует учитывать при
11.2. Оценка безубыточности деятельности фирмы
Метод оценки безубыточности основан на разделении затрат на категории: условно-постоянные и условно-переменные.
К условно-постоянным затратам относятся затраты фирмы, которые не зависят от объёма выпуска продукции. На рассматриваемом периоде времени они могут считаться постоянными. К таким затратам относятся амортизационные отчисления, заработная плата административно-управленческого персонала фирмы, плата за аренду, оплата освещения и отопления, коммерческие расходы и т.д.
К условно-переменным затратам относятся затраты фирмы, которые пропорциональны объёму выпускаемой продукции. К таким затратам относятся заработная плата рабочих, расходы на материалы и сырьё, расходы на виды энергии, используемые в технологическом процессе производства, и т.д.
При данном подходе общие затраты R определятся по формуле:
R = C +V, (11.11)
где: С – условно-постоянные затраты,
V – условно-переменные затраты.
Прибыль от продажи продукции можно оценить по следующей формуле:
ПР = В – R = В – С – V (11.12)
где: В – выручка продавцов от продажи продукции,
В выражении (11.12) выручку В можно определить по формуле:
В = Ц * Q (11.13)
Условно-переменные затраты V можно оценить по следующей формуле:
V = v * Q, (11.14)
где: v – удельные условно-переменные затраты.
С учётом (11.13) и (11.14) получим следующее выражение для определения прибыли от продажи товаров:
ПР = Ц*Q - v*Q – C = (Ц – v)*Q – C (11.15)
Построим рассматриваемые зависимости на графике рис.11.7.
 В,V,С
В,V,С


 Вmax В
Вmax В

 а V + C
а V + C

 С
С
 0 Qа Qmax Q
0 Qа Qmax Q
Рис.11.7. Определение точки безубыточности
На рисунке:
Вmax, Qmax – показатели фирмы при полном использовании всех ресурсов;
«а» - точка безубыточности, соответствующую условию В = V + C;
Qа - объём производства продукции в точке безубыточности.
Наклон линии В будет определяться ценой товара Ц. Наклон линии V+C будет определяться величиной удельных условно-переменных затрат v. Для оценки величины Qа воспользуемся уравнением (11.13) при условии ПР = 0:
Qа = С / ( Ц - v) (11.16)
Приведенные на рис. 11.7 зависимости следует рассматривать при следующих основных допущениях:
- фирма производит один товар;
- рыночной спрос на этот товар превышает максимальный объём его производства и предложения рынку;
- рыночной спрос ограничен во времени;
- постоянные затраты, цена товара и удельные условно-переменные затраты не изменяются в течение рассматриваемого периода времени производства.
Из графика на рис. 11.7 следует, что максимальная прибыль будет иметь место при полном использовании на фирме всех имеющихся ресурсов.
Рассмотрим теперь ситуацию, когда спрос ограничен и функция рыночного спроса будет иметь линейную зависимость цены Ц от объёма товаров Q. С этой целью воспользуемся ранее полученной зависимостью (11.2) Q = а – b* Ц. Подставив это выражение в формулу (11.13) получим формулу для определения прибыли ПР:
ПР = (Ц– v)*( а – b*Ц) – C (11.17)
Рассмотрим конкретный пример:
Исходные данные: Ц = 100 д.е.; v = 50 д.е.; С = 5000 д.е. ; Qmax= 160 изд.;
b = 2,5 ; 3,33; 5 изд/д. е.
По формуле (11.15) рассчитаем значение Qа в точке безубыточности:
Qа = 5000/(100 – 50) = 100 изд.
В случае неограниченного спроса при полном использовании ресурсов фирмы определим величину прибыли:
ПР = (100 – 50)*160 – 5000 = 3000 д.е.
Для учёта функции спроса условимся, что на участке изменения Q от 0 до Qа цена не будет изменяться, оставаясь равной Ц=100 д.е., а на участке от Qа до Qmax цена будет изменяться в соответствии с законом спроса (11.2). С учетом этих условий кривую спроса можно записать в следующем виде:
Q =100 – b* (Ц – 100)
В таблице 11.1 представлены результаты расчётов изменения прибыли ПР в функции Q при различных значениях коэффициента b.
| Q | |||||||
| Неограниченный спрос | |||||||
| b = 2,5 | -60 | -240 | -500 | -840 | |||
| b = 3,33 | |||||||
| b = 5 |
Из приведенных в таблице данных следует, в случае учёта линейной функции спроса прибыль может иметь на рассматриваемом участке максимум, положение которого зависит от величины коэффициента b. При b = 2,5 максимум имеет место, когда Q = 110, при b = 3,33, когда Q = 130 и при b = 5 , когда Q > 160.
Приведенный пример показывает необходимость при оценке прибыли предприятия учитывать функцию спроса.
11.3. Оптимизация ассортимента выпускаемых товаров
В основе метода оптимизации используется многопродуктовая модель производства, т.е. рассматриваемое предприятие может выпускать товары нескольких видов. При этом каждый из видов товаров проходит при изготовлении свой технологический цикл. Рассмотрим эту задачу на следующем примере: требуется определить оптимальный ассортимент товаров, изготовление и реализация которых позволит предприятию получить на рынке максимальный доход.
Таким образом, по условию задачи предприятие имеет ряд технологических линий, необходимых для изготовления нескольких видов товаров. Присвоим этим линиям соответствующие номера: линия N 1, линия N 2, линия N 3 и т.д. - всего «m» линий. Технологические линии располагают определёнными производственными мощностями соответственно В1, В2, В3 , ... , Вm . На этих линиях предприятие может изготавливать товары «n» различных видов. При изготовлении каждого из товаров осуществляется определенная последовательность разных технологических операций. Составим систему балансовых уравнений, характеризующих загрузку мощности каждой технологической линии:
 линия N 1: А11*Х1 + А12*Х2 + А13*Х3+ ………+А1nХn £ В1
линия N 1: А11*Х1 + А12*Х2 + А13*Х3+ ………+А1nХn £ В1
линия N 2: А21*Х1 + А22*Х2 + А23*Х3+ ………+А2nХn £ В2
.................................................................…………………… (11.17)
линия N m: Аm1*Х1 + Аm2*Х2 + Аm3*Х3+ ……+АmnХn £ Вm
где Аmn - удельная мощность «m»-ой линии, затрачиваемая на изготовление единицы продукции «n»-го вида;
Х - количества изготавливаемой продукции различного вида;
1,2,...,n – видовая номенклатура продукции.
Знаки неравенства в уравнениях (11.17) показывают, что загрузка каждой из линий не должна превышать располагаемых мощностей.
Для оценки экономических показателей рассматриваемого процесса используем математический аппарат методики анализа безубыточности. Если обозначить через ПРуд1, ПРуд2 …….ПРудn – прибыли от реализации, получаемые от продажи единицы товара различного вида (1, 2,..., n), где:
ПРуд1=Ц1-v1- C1/Х1;
ПРуд2=Ц2 – v1 – C2/Х2 и т.д.,
то суммарная прибыль предприятия от реализации всех товаров может быть оценена по формуле:
ПРсум= (Ц1-v1)*Х1+ (Ц2 – v2)*Х2 +……. – (С1+С2+С3+…), (11.18)
где: Ц1,Ц2…Цn – цены разных видов выпускаемой продукции;
v1, v2.. vn – удельные переменные затраты по видам выпускаемой продукции;
С1,С2… Cn – постоянные затраты, относимые на различные виды выпускаемой продукции.
В затратах учитываются производственные издержки (себестоимость), коммерческие и управленческие расходы.
Зависимость (11.18) может использоваться для формирования целевой функции.
Цель состоит в том, чтобы определить ассортимент товаров (1,2,...,n) и значения объемов их выпуска (Х1, Х2, Х3……. ), при которых суммарная прибыль от реализации ПРсум будет иметь максимальное значение.
Эта задача может быть решена методами линейного программирования. Рассмотрим вариант использования графического метода линейного программирования. С этой целью упростим условия задачи до двухмерного уровня: m = 2 и n = 2. Система балансовых уравнений и целевой функции примут следующий вид:
1. А11*Х1 + А12*Х2 £В1
2. А21*Х1 + А22*Х2 £ В2 (11.19)
3. ПРсум= (Ц1-v1)*Х1+ (Ц2-v2)*Х2 – (С1+С2)
Результаты решения такой системы представлены на графике рис.11.8:
Фигура АВСО на графике определяет область возможных решений Х1 и Х2. Точка «В» отвечает условию получения максимальной прибыли ПРмакс. Эта точка определяет искомые решения Х1опт и Х2опт. Часто для упрощения процедуры анализа в качестве критерия вместо показателя ПРмакс используется максимальная величина суммарной выручки Вмакс. В этом случае последнее уравнение системы (11.19) можно записать в следующем виде:
В = Ц1*Х1+ Ц2*Х2,
где: В - суммарная выручка предприятия от продажи товаров.

Рис. 11.8. Решение задачи методом линейного программирования
Недостаток данного подхода в том, что при этом не учитываются производственные издержки.
Рассмотрим числовой пример с использованием в качестве критерия максимальной прибыли.
Пример. Предприятие производит два вида чехлов (обозначим их «А» и «В») спортивного назначения.
При изготовлении чехлов осуществляются следующие технологические операции:
1. Раскрой и окраска материала (РиО)
2. Шитье чехлов (Ш)
3. Заключительная операция (З)
4. Контроль и упаковка чехлов (КиУ).
Удельные трудоемкости этих операций в нормо-часах представлены в следующей таблице:
| Продукция | РиО | Ш | З | КиУ |
| Чехол «А» | 7/10 | 1/2 | 1/10 | |
| Чехол «В» | 5/6 | 2/3 | 1/4 |
Обозначим:
Х1 - искомое число чехлов «А»;
Х2 - искомое число чехлов «В».
Продажная цена чехла «А» равна 15 д.е., удельные переменные затраты vA = 5 д.е., постоянные затраты, относимые на производство чехлов «А», в расчёте на месяц СA = 200 д.е.
Продажная цена чехла «В» равна 13 д.е., удельные переменные затраты vв = 4 д.е., постоянные затраты, необходимые для производства чехлов «В», в расчёте на месяц Св = 300 д.е.
Прибыль предприятия от реализации чехлов за месяц при производстве обеих видов чехлов может быть определена по следующей формуле:
ПРсум = (15-5)*Х1 + (13-4)*Х2 – (200+300)=10*Х1+9*Х2-500
| Операции | «РиО» | «Ш» | «З» | «КиУ» |
| Располагаемые мощности (в нормо-часах) |
Располагаемые мощности за месяц в нормо-часах представлены в следующей таблице:
На основе приведенных данных можно составить следующую систему балансовых уравнений:
1. 7/10*Х1+ Х2 £ 630
2. 1/2*Х1+ 5/6*Х2 £ 600
3. Х1 + 2/3*Х2 £ 708 (11.20)
4. 1/10*Х1+ ¼*Х2 £135
5. Х1, Х2 ³ 0
Условие достижения максимальной прибыли предприятия от реализации (целевая функция) можно записать в следующем виде:
(10*Х1 + 9*Х2 -500) è max (11.21)
Рассмотрим решение задачи графическим методом линейного программирования. Решение представлено на графике рис.11.9. На графике образовалась фигура ABCDO.
Подставляя в целевую функцию (11.21) координаты точек «А», «В», «С» и «D» фигуры АВСDО определим, что в точке «С» целевая функция будет иметь максимальное значение. Координаты точки «С» имеют следующие значения:
Х1опт = 540 шт; Х2опт = 252 шт.
Прибыль предприятия в точуе «С» составит ПРмакс = 7668 – 500 = 7168 д.е. При всех других вариантах (точки А,В и D) прибыль будет меньше. На графике уравнение 10*Х1+9*Х2 = 7668 д.е проходит через точку «С» фигуры АВСDО.
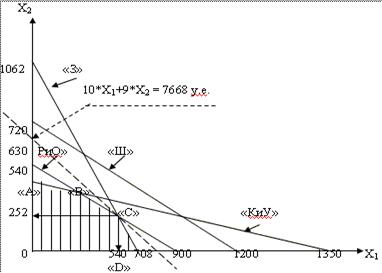
Рис. 11.9. Решение задачи оптимизации производства чехлов
Определим степень использования располагаемых мощностей технологических линий в случае реализации оптимального решения:
| Технологические операции | Расчётные формулы | Используемые мощности (час) | Неиспользованные мощности (час) |
| РиО | 7/10*540+1*252 | ||
| Ш | ½*540+5/6*252 | ||
| З | 1*540+2/3*252 | ||
| КиУ | 1/10*540+1/4*252 |
Из таблицы видно, что технологическая линия «Ш» будет существенно недогружена (120 часов), небольшая недогрузка будет иметь место также на технологической линии «КиУ» (18 часов). Руководство предприятия должно учесть эти данные при окончательном планировании работы цеха.
В рассмотренном случае ассортимент товаров фирмы должен включать два вида, но это справедливо не всегда.
Предположим, что спрос рынка на чехол «А» существенно упал и чтобы сохранить производство цена на этот чехол была уменьшена с 15 до 10 д.е..Тогда при сохранении тех же балансовых уравнений целевая функция будет иметь следующий вид:
(5*Х1+ 9*Х2 - 500 ) è max
Используя прежний методический подход определим, что в этом случае оптимальное решение будет иметь место в точке «В», что соответствует Х1опт = 300 шт., Х2опт = 420 шт. Прибыль от реализации будет равна: ПРмакс = 5*300 + 9*420 – 500 = 4780 д.е.
Рассмотрим еще один вариант этой задачи.
Допустим, что руководством фирмы на основе маркетинговых исследований принято решение о необходимости производства чехлов в следующих количествах:
чехол «А» - 500 шт., чехол «В» - 360 шт.
Какие в этом случае понадобятся дополнительные ресурсы? Результаты расчетов представлены в следующей таблице:
| Технологические операции | Расчётные формулы | Потребные мощности (час) | Дополнительные мощности (час) |
| РиО | 7/10*500+1*360 | ||
| Ш | ½*500+5/6*360 | Не требуется | |
| З | 1*500+2/3*360 | ||
| КиУ | 1/10*500+1/4*360 |
Из таблицы видно, что существенные дополнительные ресурсы в этом случае потребуются для первой (РиО) и третьей (З) технологических операций.
При существенном различии цен на чехлы «А» и В» целевая функция может стать максимальной в точках «А» или «D» графика. В этих случаях оптимальный ассортимент товаров фирмы будет состоять только из товара «А», или только из товара «В». Читателю предлагается провести самостоятельные исследования этих вариантов.
11.4. Оптимальное распределение товаров по целевым рынкам
Рассмотрим деятельность компании, которая имеет два производственных предприятия, выпускающих идентичные товары и расположенных в различных городах. Товары этих предприятий могут реализовываться на трех целевых рынках, расположенных в разных географических регионах, куда они доставляются различными видами транспорта. Ёмкости целевых рынков ограничены. Компания заинтересована, чтобы при условии полной реализации продукции предприятий суммарные транспортные расходы компании по доставке товаров на целевые рынки были минимальными.
Таким образом, задача заключается в оптимальном распределении потоков товаров по рынкам при условии, что емкости рынков должны быть полностью использованы. Описанная ситуация представлена на следующей схеме:

Рис. 11.10 Схема распределения товаров по рынкам
П1, П2 – мощности предприятий по производству товаров;
Р1, Р2, Р3 - ёмкости рынков;
Х11…….Х23 - искомые потоки товаров.
Исходные данные представлены ниже:
П1= 20 000 шт., П2= 30 000 шт.
Р1 = 10 000 шт., Р2 = 30 000 шт., Р3= 10 000 шт.
Удельные стоимости перевозок товаров (у.е./шт.) приведены в следующей таблице:
| С11 | С12 | С13 | С21 | С22 | С23 |
С учётом приведенных данных составим систему балансовых уравнений:
 Х11 + Х12 +Х13 = 20000
Х11 + Х12 +Х13 = 20000
Х21 + Х22 + Х23 = 30000 (11.22)
Х11 + Х21 = 10000
Х12 + Х22 = 30000
 Х13 + Х23 =10000
Х13 + Х23 =10000
Формула для определения суммарных затрат «R» компании на перевозки товаров (целевая функция) будет иметь следующий вид:
R = 4*Х11 + 9*Х12 +3*Х13+4*Х21 + 8*Х22 + 1*Х23 (11.23)
Дата добавления: 2014-12-03; просмотров: 1349;
