Требуется определить значения Х11,Х12 ,Х13, Х21,Х22 и Х23 при условии, что целевая функция «R» будет иметь минимальное значение.

Для решения используем графический метод линейного программирования.

В качестве свободных неизвестных в данном случае выберем Х₁₁ и Х₁₂. Тогда остальные неизвестные можно выразить через эти свободные неизвестные с помощью следующих зависимостей:

Х₁₃ = 20000 - Х₁₁ - Х₁₂

Х₂₁ = 10000 - Х₁₁

Х₂₂ = 30000 - Х₁₂

Х₂₃ = 10000 – Х₁₃ = -10000 + Х₁₁ + Х₁₂

Поскольку по условию задачи Х₁₃≥ 0, Х₂₁≥0, Х₂₂≥0, Х₂₃≥0, то можно получить следующую систему неравенств, необходимых для линейного программирования::

1. 20000 - Х₁₁ - Х₁₂ ≥ 0

2. 10000 - Х₁₁≥ 0

3. 30000 - Х₁₂ ≥ 0 (11.24)

4. -10000 + Х₁₁ + Х₁₂≥ 0

5. Х₁₁≥ 0, Х₁₂≥ 0

Целевая функция будет иметь следующий вид:

(4*Х₁₁ + 9*Х₁₂ +3*Х₁₃+4*Х₂₁ + 8*Х₂₂ + 1*Х₂₃) è min

Решение представлено на графике рис. 11.11.:

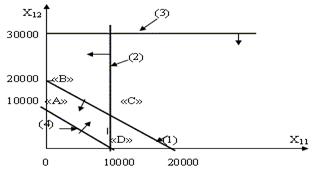
На основе полученных данных можно определить суммарные расходы по перевозке товаров на выбранные рынки:

Минимальное значение суммарных расходов компания будет иметь в точке «С». В результате оптимальный план реализации товаров на данных рынках будет следующим:

Х₁₁= 10000, Х₁₂ =10000, Х₁₃ =0,

Х₂₁= 0, Х₂₂=20000, Х₂₃ = 10000.