Анализ пропорционального контроллера

Давайте рассмотрим простой процесс в стабильном состоянии. Используем пропорциональный контроллер.

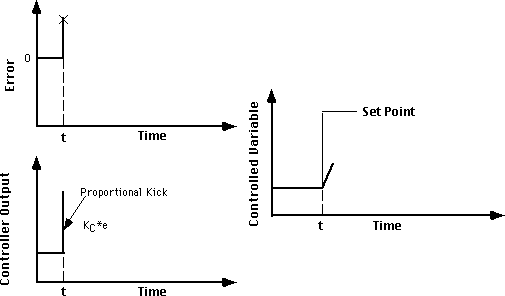
В стабильном состоянии значение PV равно значению SP, поэтому отклонение равно нулю, а выход контроллера остается неизменным.

Предположим, что в момент t мы увеличиваем уставку, что приводит к увеличению отклонения. В зависимости от того, является ли контроллер прямого или обратного действия, пропорциональный контроллер увеличивает или уменьшает свой выходной сигнал на величину, пропорциональную величине отклонения. Мы изучим прямое и обратное действие позже. Предположим, что контроллер настроен на обратное действие.

Пропорциональный контроллер обратного действия будет увеличивать свой выходной сигнал, чтобы увеличить контролируемое значение, PV.

Скачкообразное изменение уставки в момент t приводит к мгновенному увеличению отклонения. В итоге пропорциональный контроллер немедленно увеличивает свой выход на величину равную отклонению, умноженному на KC. Такой начальный скачок выходного сигнала контроллера известен как пропорциональный бросок.

При увеличении PV отклонение уменьшается, и в результате выходной сигнал контроллера также увеличивается пропорционально.

Контролируемая переменная продолжает увеличиваться и достигает своей уставки. После этого она достигает нового стабильного состояния.

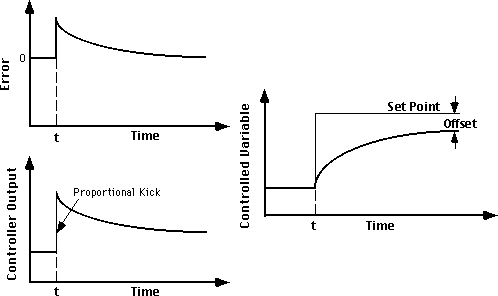
Однако, это новое значение стабильного состояния не равно уставке. Данное отклонение контролируемой переменной от своей уставки в стабильном состоянии называется "установившейся ошибкой".

Можно ли избежать установившейся ошибки?

К сожалению, избежать установившейся ошибки невозможно. Это присущий недостаток пропорционального контроллера. Пропорциональный контроллер определенно способен понизить установившуюся ошибку, если установить пропорциональное усиление на более высокое значение. По мере увеличения усиления установившаяся ошибка уменьшается.

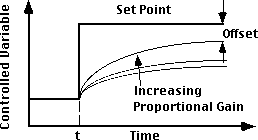
Теперь возникает другой вопрос: "Почему бы не увеличивать пропорциональное усиление до тех пор, пока установившаяся ошибка не будет устранена?"

Для процесса первого порядка с помощью увеличения усиления можно уменьшать установившуюся ошибку и получить приемлемую реакцию контроллера. Но к сожалению, большинство процессов реального мира более сложные, например, системы высшего порядка с "мертвым" временем. Обычно, когда усиление превышает определенное значение, контролируемая переменная начинает колебаться. Если увеличить усиление еще больше, контролируемая переменная становится неустойчивой.

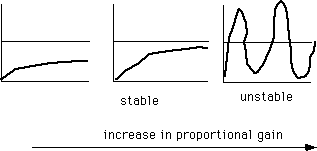
Поэтому для устойчивого управления очень важно выбрать верное значение для пропорционального усиления. Метод определения подходящих значений для параметров контроллера называется "настройка".

Несмотря на присущий недостаток сохранения установившейся ошибки, пропорциональный контроллер имеет привлекательность в ряде практических условий управления, поскольку он относительно устойчив. Например, в некоторых процессах управления уровнем поддержание уровня жидкости близко к уставке не так важно, так как складской резервуар не переливается и не пересыхает. В этом случае установившаяся ошибка не составляет проблемы.

Устранить установившуюся ошибку можно, только введя в систему интегральный термин, о котором мы узнаем далее.

Пропорциональный диапазон

Иногда пропорциональную постоянную описывают другим термином, который называется "пропорциональный диапазон", который имеет следующее определение.

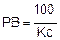
где:

PB — пропорциональный диапазон

K_C — пропорциональное усиление

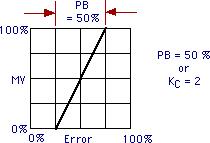
Пропорциональный диапазон представляет собой изменение отклонения в процентах, необходимое, чтобы изменить выход контроллера на 100%. Например, PB = 50 означает, что требуется отклонение в 50% для того, чтобы переместить MV на 100%.

При этом важно понимать, что действие увеличения или уменьшения пропорционального диапазона противоположно действию пропорционального усиления. Когда пропорциональный диапазон уменьшается, пропорциональное действие становится больше. Если пропорциональный диапазон очень низкий, контролируемая переменная может стать колебательной и, в конце концов, неустойчивой.