Интегральный

Мы узнали о том, что пропорциональный контроллер не может полностью устранить отклонение. Существует установившаяся ошибка. Эту ошибку можно устранить, если алгоритм управления включает дополнительный термин для изменения выхода контроллера, пока существует отклонение.

Дополнительный термин называется "интегральная составляющая".

Контроллер, имеющий только интегральную составляющую, называется интегральным контроллером или просто I-контроллером.

С математической точки зрения интегральное действие имеет следующее выражение:

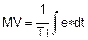
где:

T_I — время интегрирования, которое называют "время возврата".

В системе Лапласа это выражается следующим образом:

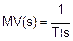
Действие I-контроллера можно понять лучше, если изменить интегральное уравнение. Дифференцировав обе стороны уравнения относительно времени, мы получаем

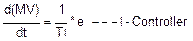
Левая часть уравнения это скорость изменения выхода контроллера. Таким образом, для I­контроллера скорость изменения выхода пропорциональна отклонению.

Это значит, что для I-контроллера выход контроллера продолжает увеличиваться или уменьшаться, пока существует отклонение.

В результате, установившаяся ошибка будет устранена. Выход остается без изменения, только когда отклонение равно нулю.

Давайте вспомним, что для P-контроллера изменение выхода контроллера пропорционально отклонению.

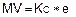--- P-контроллер

Хотя устранение установившейся ошибки — важная задача управления, I-контроллер редко используют сам по себе, так как до тех пор, пока отклонение не будет сохраняться в течение какого-то времени, происходит очень слабое управляющее действие. Напротив, P-контроллер начинает действовать немедленно, как только установлено наличие отклонения. По этой причине интегральное управление обычно применяется в сочетании с пропорциональным управлением, чтобы получить более качественное управление в целом.