Правило Лопиталя

Теорема. Пусть функции f₁(x) и f₂(x) определены и дифференцируемы в некоторой окрестности точки х₀, за исключением, быть может, самой точки х₀. Кроме того, пусть также =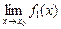
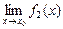= = 0 или 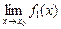= 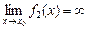, причем 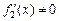в указанной окрестности точки х₀.

Тогда, если существует предел отношения 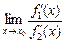(конечный или бесконечный), существует и предел 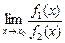, причем справедлива формула = .

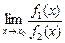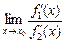Замечание 1. При необходимости правило Лопиталя может быть применено два и более раз.

Замечание 2. Теорема остается верной и в случае, когда ( ).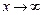

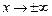Пример. 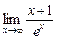= = 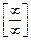= = 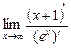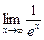0.