Производная сложной функции. Если переменная у — функция от переменной и, т
Если переменная у — функция от переменной и, т. е. y = f(и), а переменная и = 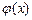 — функция от переменной х, то говорят, что задана сложная функция у =
— функция от переменной х, то говорят, что задана сложная функция у = 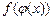 .
.
Теорема. Если функции y = f(и), и = 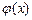 дифференцируемы, то производная сложной функции существует и может быть вычислена по формуле
дифференцируемы, то производная сложной функции существует и может быть вычислена по формуле 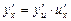 .
.
Таблица производных
1. (un)' = n · un – 1 · u', (n 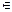 R).
R).
2. 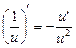 .
.
3. 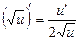 .
.
4. 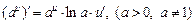 .
.
5. (eu)' = eu · u'.
6. 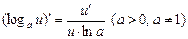 .
.
7. (ln u)' = 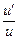 .
.
8. (sin u)' = cos u · u'.
9. (cos u)' = –sin u · u'.
10. (tg u)' = 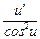 .
.
11. (ctg u)' = 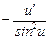 .
.
12. (arcsin u)' = 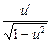 .
.
13. (arccos u)' = 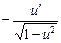 .
.
14. (arctg u)' = 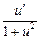 .
.
15. (arcctg u)' = – 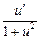 .
.
Дата добавления: 2014-12-02; просмотров: 839;
