Типовая задача 5
Вычислить пределы следующих функций:
1) 
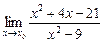при а) х0 = 2; б) х0 = 3; в) х0 = 
;
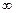2) 
;
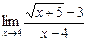3) 
;
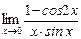4) 
.
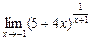Решение. 1а) Функция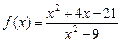 
является элементарной и определенной в точке х0 = 2. По теореме о пределе для элементарной функции,
= 
= 
.
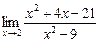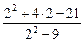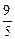1б) Если применить теоремы о пределах сразу, то получим неопределенность типа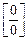 
, поэтому преобразуем числитель и знаменатель функции:
= = 
= 
= 
= 
.
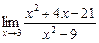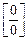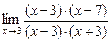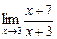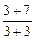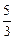1в) Применив теоремы о пределах сразу, получим неопределенность типа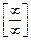 
. Поэтому для предварительного преобразования выражения функции разделим числитель и знаменатель на старшую степень переменной, т. е. на х2:
= = 
=
= 
= 
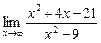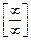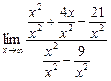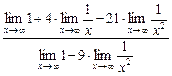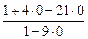= 1.
2) Если будем применять теоремы о пределах сразу, то получим неопределенность типа 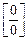. Для преобразования функции умножим числитель и знаменатель дроби на выражение 
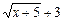, сопряженное числителю:
= = 
=
= 
= 
=
= 
= 
= 
.
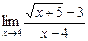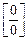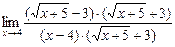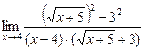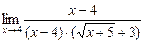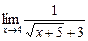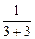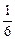3) Применив очевидные преобразования и первый замечательный предел, получим:
= = 
= 
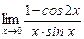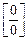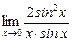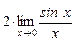= 2 · 1 = 2.
4) При применении теорем о пределах сразу, получаем неопределенность типа [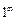 
]. Применяя второй замечательный предел, получим:
= [ ] = 
=
= 
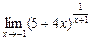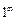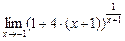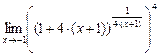= е4.
Ответ: 1а) 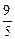; 1б) 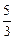; 1в) 1; 2) 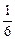; 3) 2; 4) е4.
4. Задания 6 и 7
по теме «Производная и ее применение
для исследования функций»
Дата добавления: 2014-12-02; просмотров: 785;