Понятие производной
Производной функции y = f(x) в точке х0 называется предел 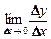 =
=
= 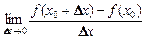 отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.
отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.
Производная функции y = f(x) обозначается через 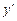 , f'(x),
, f'(x), 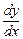 .
.
Процесс нахождения производной функции называется ее дифференцированием.
Функция y = f(x) называется дифференцируемой в точке х0, если она в этой точке имеет конечную производную.
Теорема. Если функция y = f(x) дифференцируема в точке х0, то она непрерывна в этой точке.
Обратное утверждение, вообще говоря, неверно.
Геометрический смысл производной функции y = f(x) в точ-
ке х0 состоит в том, что производная в точке х0 f'(x0) равна тангенсу угла 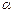 наклона касательной к графику функции y = f(x) в точке
наклона касательной к графику функции y = f(x) в точке
с абсциссой х0 (рис. 11).
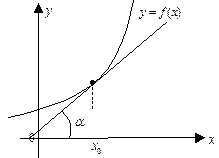
|
| Рис. 11 |
В экономике существует несколько интерпретаций производной. Среди них можно упомянуть следующие:
1. Предельный доход определяется как производная от суммарного дохода R по количеству товара Q.
2. Предельные издержки определяются как производная издержек производства R по количеству товара Q.
Таким же образом определяются предельная выручка, предельный продукт и другие предельные величины, характеризующие не состояния, а процесс изменения какого-либо экономического показателя.
Правила вычисления производных:
1. Производная постоянной функции равна нулю, т. е. c' = 0.
2. Производная независимого аргумента х равна 1, т. е. х' = 1.
3. Производная алгебраической суммы дифференцируемых функций равна соответствующей алгебраической сумме производных функций-слагаемых, т. е. 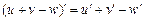 .
.
4. Производная произведения двух дифференцируемых функций u
и v вычисляется по формуле 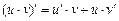 .
.
Следствие. Постоянный множитель можно вынести за знак производной, т. е. (с · u)' = с · u'.
5. Производная частного дифференцируемых функций u и v вычисляется по формуле 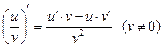 .
.
Дата добавления: 2014-12-02; просмотров: 1135;
