Теоремы о пределах
1. Функция y = f(x) в точке х0 не может иметь более одного предела.
2. Предел постоянной величины равен самой этой величине, т. е. 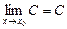 .
.
3. Пусть f1(x) и f2(x) — функции, для которых существуют пределы при 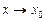 :
: 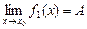 ,
, 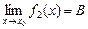 .
.
Тогда:
3.1. Существует и предел алгебраической суммы этих функций, причем предел этой алгебраической суммы равен алгебраической сумме пределов, т. е.
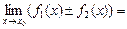
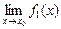
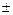
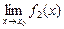 = А
= А 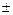 В.
В.
3.2. Существует и предел произведения этих функций, причем предел этого произведения равен произведению этих пределов:
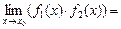
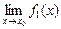 ·
· 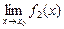 = А·В.
= А·В.
3.3. Если В  0, то существует и предел частного этих функций, причем предел этого частного равен частному пределов, т. е.
0, то существует и предел частного этих функций, причем предел этого частного равен частному пределов, т. е.
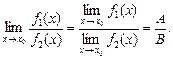
Формулировка для случая, когда 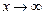 , аналогична.
, аналогична.
Функция g(x) называется бесконечно малой функцией при 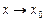 (
( 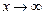 ), если
), если
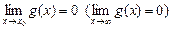 .
.
Функция f(x) называется бесконечно большой функцией при 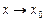 (
( 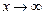 ), если для любого Р > 0 найдется положительное число
), если для любого Р > 0 найдется положительное число 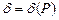 , что для всех
, что для всех 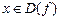 , удовлетворяющих условию
, удовлетворяющих условию 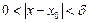 (
( 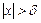 ), выполняется неравенство
), выполняется неравенство 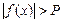 . Обозначение:
. Обозначение: 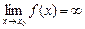 (
( 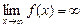 ).
).
Если f(x) 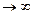 при
при 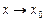 и f(x) принимает только положительные (отрицательные) значения, то пишут
и f(x) принимает только положительные (отрицательные) значения, то пишут
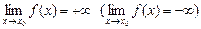 .
.
Теорема (о связи между бесконечно малыми и бесконечно большими функциями)
Если g(x) — бесконечно малая функция при 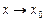 (
( 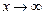 ), то
), то 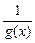 — бесконечно большая функция при
— бесконечно большая функция при 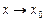 (
( 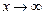 ).
).
Если f(x) — бесконечно большая функция при 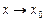 (
( 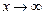 ), то
), то 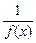 — бесконечно малая функция при
— бесконечно малая функция при 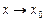 (
( 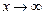 ).
).
Дата добавления: 2014-12-02; просмотров: 910;
