Предел и непрерывность функции

Пусть X и Y — некоторые множества, и пусть каждому 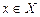поставлен в соответствие по определенному правилу f единственный элемент 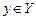. Тогда говорят, что на множестве X задана функция одной переменной со значениями в множестве Y. Обозначение: y = f(x). В этом случае X — область определения функции. Обозначение: D(f).

Всякий интервал, содержащий точку x₀, называется окрестностью точки x₀.

Пусть 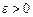. Интервал (x₀ – ; x₀ + ) называется -окрестностью точки x₀.

Определение предела функции по Коши. Пусть функция y = f(x) определена в -окрестности точки x₀ за исключением, быть может, точки x₀. Тогда, если для любого 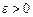, сколь угодно малым бы оно ни было, существует такое 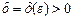, что для всех 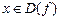, удовлетворяющих неравенству 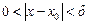, выполняется неравенство 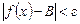, то число B называется пределом функции в точке x₀. Обозначение: .

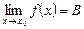Число В называется пределом функции f(x) в бесконечности, если для любого даже сколь угодно малого положительного числа 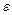найдется такое 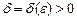, что для всех 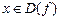, удовлетворяющих неравенству 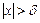, выполняется неравенство 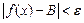. Обозначение: .

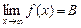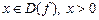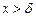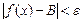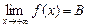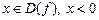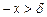Если для всех и выполняется неравенство , то . Если для всех и выполняется неравенств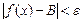о , то .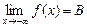

Рассмотрим 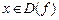, 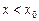( 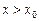). Если существует предел функции при х, стремящемся к х₀, то он называется левым (правым) пределом функции в точке х₀. Обозначение: .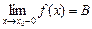

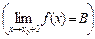Факт существования в точке х₀ предела функции у = f(x) равносилен факту существования в этой точке равных между собой односторонних пределов .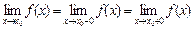

Функция y = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению 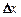аргумента в этой точке соответствует бесконечно малое приращение 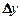функции (рис. 10).

Рис. 10

Функция y = f(x) называется непрерывной в точке х₀, если предел функции в точке х₀ равен значению функции в этой точке, т. е. .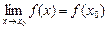

Функция f(x) называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.

Точки, в которых функция не является непрерывной, называются точками разрыва функции.