Типовая задача 3
Даны векторы 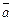 = (2;–1;3),
= (2;–1;3), 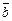 = (1;2;–3),
= (1;2;–3), 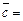 (0;1;2),
(0;1;2), 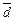 = (–1;9;–13)
= (–1;9;–13)
со своими координатами в базисе 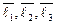 . Показать, что векторы
. Показать, что векторы 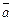 ,
, 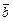 ,
, 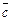 сами образуют базис, и найти разложение вектора
сами образуют базис, и найти разложение вектора 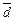 в новом базисе.
в новом базисе.
Решение. Вычисляем определитель, составленный из координат этих векторов: 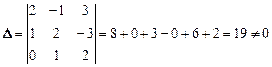 .
.
По теореме 1, сформулированной выше, векторы 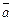 ,
, 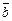 ,
, 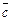 образуют базис пространства R3.
образуют базис пространства R3.
Пусть 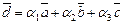 — разложение вектора
— разложение вектора 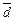 по базису
по базису 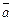 ,
, 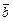 ,
, 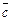 .
.
По условию задачи имеем:
–1· 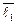 + 9 ·
+ 9 · 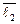 – 13 ·
– 13 · 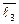 =
= 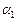 · (2 ·
· (2 · 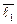 – 1 ·
– 1 ·  + 3·
+ 3· 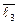 ) +
) +
+ 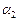 · (1 ·
· (1 · 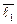 + 2 ·
+ 2 ·  – 3 ·
– 3 · 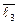 ) +
) + 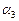 · (0 ·
· (0 · 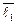 + 1 ·
+ 1 · 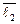 + 2·
+ 2· 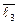 ),
),
–1· 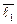 + 9 ·
+ 9 ·  – 13 ·
– 13 · 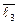 = (2 ·
= (2 · 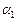 + 1 ·
+ 1 · 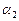 + 0 ·
+ 0 · 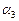 ) ·
) · 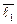 +
+
+ (–1 · 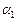 + 2 ·
+ 2 · 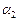 + 1 ·
+ 1 · 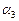 ) ·
) ·  + (3 ·
+ (3 · 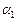 – 3 ·
– 3 · 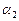 + 2 ·
+ 2 · 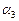 ) ·
) · 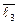 .
.
Из условия равенства двух векторов получим:
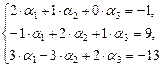
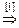
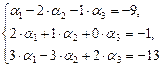
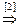
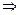
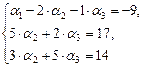
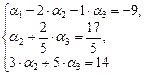
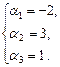
[1]: Обе части второго уравнения умножим на (–1). Поменяем местами первое и второе уравнения.
[2]: Обе части первого уравнения умножим на (–2) и прибавим соответственно ко второму уравнению. Затем обе части первого уравнения умножим на (–3) и прибавим соответственно к третьему уравнению.
[3]: Обе части второго уравнения разделим на 5.
[4]: Обе части второго уравнения умножим на (–3) и прибавим соответственно к третьему уравнению. Из третьего уравнения системы 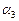 = 1. Подставим это значение во второе уравнение и получим
= 1. Подставим это значение во второе уравнение и получим 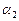 = 3. Подставляя полученные значения
= 3. Подставляя полученные значения 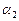 = 3,
= 3, 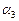 = 1 в первое уравнение, найдем
= 1 в первое уравнение, найдем 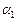 = –2.
= –2.
Итак, 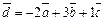 .
.
Ответ: 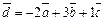 .
.
Дата добавления: 2014-12-02; просмотров: 806;
