Применение определителей
Теорема 1. Векторы 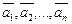 тогда и только тогда образуют базис пространства Rn, когда определитель
тогда и только тогда образуют базис пространства Rn, когда определитель 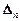 , образованный из координат этих векторов, отличен от нуля.
, образованный из координат этих векторов, отличен от нуля.
Матрица В называется обратной матрицей по отношению к матрице А (4), если их произведение равно единичной матрице:
АВ = ВА = Е.
Для матрицы В, обратной по отношению к А, существует специальное обозначение A–1.
Теорема 2. Квадратная матрица (4) тогда и только тогда имеет обратную, если ее определитель (5) отличен от нуля.
Справедлива следующая формула для нахождения обратной матрицы:
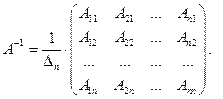 (6)
(6)
Пример. Пусть 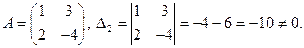
Матрица А имеет обратную:
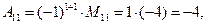
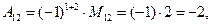
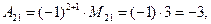
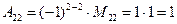 .
.
Тогда
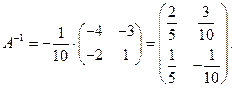
Дата добавления: 2014-12-02; просмотров: 1147;
