Определители. Квадратной матрице А порядка п можно сопоставить число det A (или |A|, или ), называемое ее определителем

Квадратной матрице А порядка п можно сопоставить число det A (или |A|, или 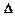), называемое ее определителем, следующим образом:

1. Если п = 1, A = (a₁₁), тогда определитель первого порядка имеет вид

|A| = 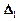= |a₁₁| = a₁₁.

2. Если п = 2, 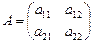, тогда определитель второго порядка вычисляется по формуле

.

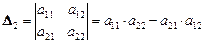3. Если п = 3, 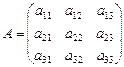, то матрице третьего порядка соответствует определитель

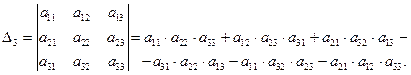
Это выражение получается по правилу треугольников (правилу Саррюса). Его можно пояснить схемами, на которых элементы, входящие в одно произведение с указанным знаком, соединены отрезками (рис. 9).

Рис. 9