Определители n-го порядка

Определитель n–го порядка состоит из n² элементов, записанных в n строк и в n столбцов, и имеет вид:

.

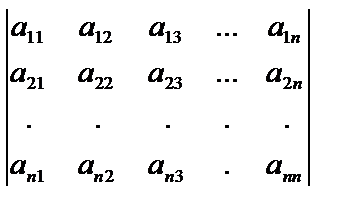Элемент определителя а_ij стоит в строке с номером i и в столбце с номером j. Индексы i и j могут принимать любые натуральные значения от 1 до n. Так, записав а_i3(i=1,2,…,n), мы перечислим все элементы, стоящие в столбце с номером 3: а₁₃, а₂₃, а₃₃,…,а_n3. Элементы а_ij (при i=j) составляют главную диагональ определителя.

Вычисление определителя n-го порядка сводится к вычислению определителей третьего и второго порядка при помощи следующих свойств.

Свойства определителей:

1. Определитель не изменится, если его строки заменить столбцами (не меняя порядка их номеров). Поэтому далее будем говорить о строках, подразумевая сказанное верным и для столбцов.

2. Если поменять местами две строки определителя, то он изменит свой знак.

3. Определитель с двумя одинаковыми (или пропорциональными) строками равен нулю.

4. Общий множитель всех элементов какой-либо его строки можно выносить за знак определителя.

5. Если все элементы какой-либо строки определителя равны нулю, то такой определитель равен нулю.

6. Определитель не изменится, если ко всем элементам какой-либо его строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

Примеры.

№ 6. Вычислить определители:

а)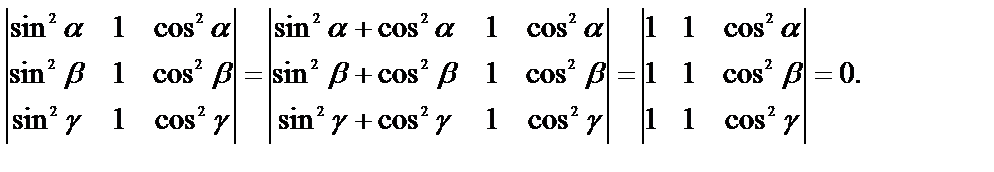

Здесь к элементам первого столбца прибавили элементы третьего столбца.

б)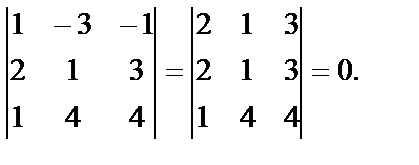

К элементам первой строки прибавили элементы третьей.

в)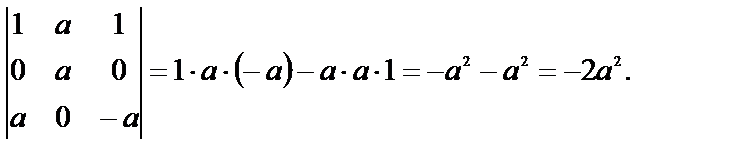

Этот определитель удобнее вычислять по правилу Сарруса, т.к. четыре из шести слагаемых равны нулю.

Вернемся к свойствам определителей. Но введем вначале понятия минора и алгебраического дополнения.

Если из данного определителя n-го порядка вычеркнем строку и столбец, на пересечении которых стоит элемент а_ij, то получим определитель (n-1)-го порядка, который называется минором элемента а_ij и обозначается М_ij. Например, в определителе третьего порядка 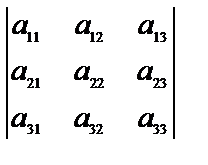найдем минор М₂₁ элемента а₂₁. Для этого вычеркиваем вторую строку и первый столбец: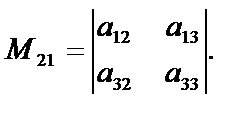

В определителе четвертого порядка можно записать 4х4=16 миноров, каждый из которых будет определителем третьего порядка.

Запишем миноры элементов а₃₂ и а₄₄, например, определителя четвертого порядка:

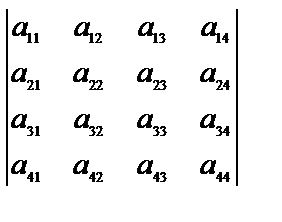
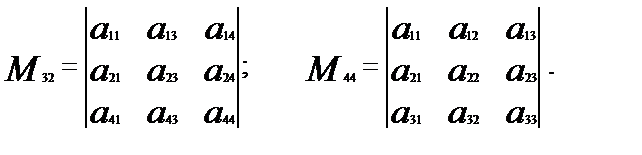
Алгебраическим дополнением элемента а_ij называется его минор, взятый со знаком (–1)^i+j, и обозначается А_ij. Таким образом, А_ij=(–1)^i+j×М_ij.

Найдем, например, алгебраические дополнения элементов определителя .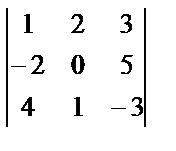

.

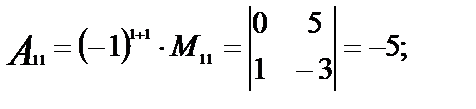
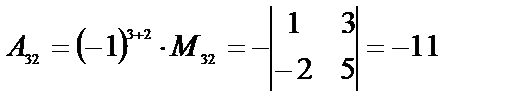Рассмотрим, наконец, свойство о разложении определителя по строке или столбцу.

7. Определитель равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения.

Так, определитель третьего порядка, например, можно вычислить при помощи трех определителей второго порядка:

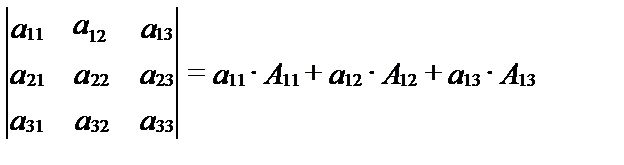- разложение по элементам первой строки.

Следствие. Если все элементы какой-либо строки (столбца), кроме одного, равны нулю, то определитель равен произведению отличного от нуля элемента на его алгебраическое дополнение.

Поэтому, например,

№.7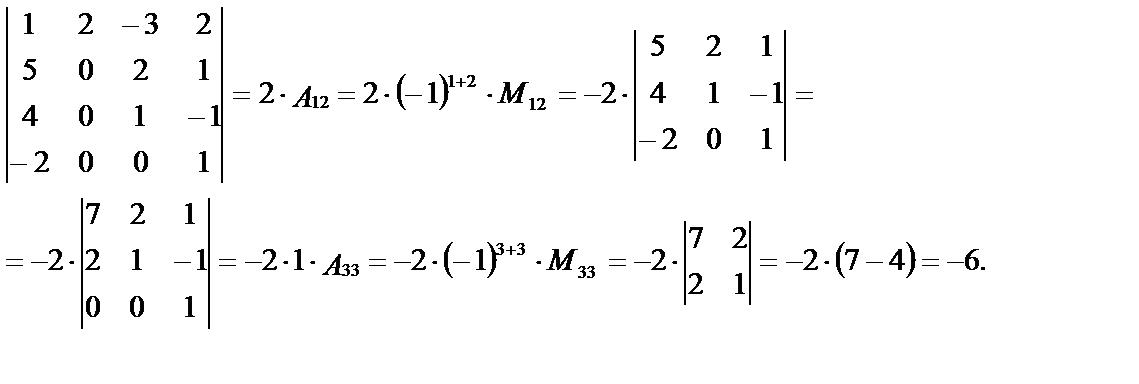

В определителе третьего порядка мы к элементам первого столбца прибавили соответствующие элементы третьего, умноженные на 2.

Итак, с помощью свойств определителя можно разложить определитель любого порядка по строке или столбцу. Последовательно понижая порядок, вычислим определитель непосредственно, применив правило для вычисления определителя третьего или второго порядка.

Рассмотрим определители особого вида: диагональный и треугольный.

Диагональным определителем называется определитель, диагональные элементы которого отличны от нуля, а все остальные элементы равны нулю.

Треугольным определителем называется определитель, все элементы которого, расположенные ниже (или выше) главной диагонали, равны нулю.

№ 8 Вычислить диагональный определитель n-го порядка

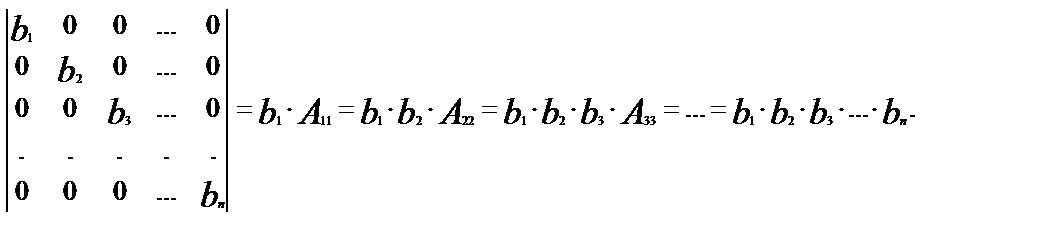
Раскладывая определитель по элементам 1^го столбца, мы получили произведение 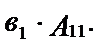Но определитель (n–1)-го порядка А₁₁ таким же образом представим в виде произведения 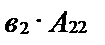и т.д.

Таким образом, диагональный определитель равен произведению элементов его главной диагонали.

Легко показать, что и треугольный определитель равен произведению элементов его главной диагонали:

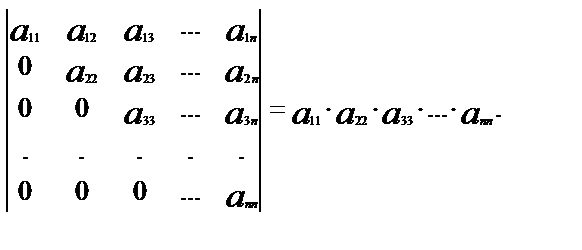
№ 9 Вычислить определители:

1)

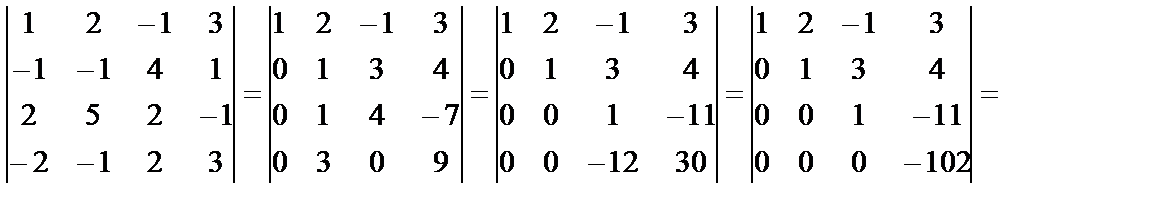
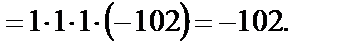
2) 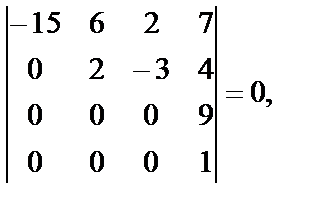т.к. в треугольном определителе один из элементов главной диагонали равен нулю.

Два рассмотренных в примере № 9 определителя мы свели к треугольной форме, получая в столбцах нули с помощью 6^го свойства определителей.

Покажем, как еще можно вычислить определитель, применяя изложенные свойства.

3)

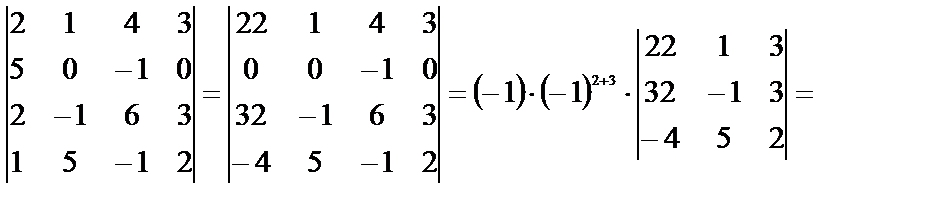
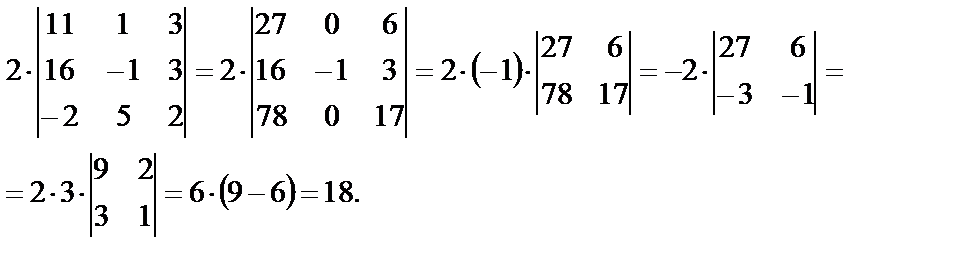
Опишем наши действия. В данном определителе привлекательна вторая строка, т.к. она уже содержит два нуля. Умножив все элементы 3-го столбца на 5, прибавим их к соответствующим элементам 1-го столбца. Полученный определитель равен произведению отличного от нуля элемента –1 на его алгебраическое дополнение А₂₃. Из первого столбца определителя 3-го порядка вынесем общий множитель 2 и получим нули во 2-м столбце, сложив 1-ю строку со второй, затем, сложив 3-ю строку со второй, умноженной на 5. Полученный определитель второго порядка можно упростить, сложив 2-ю строку с первой, умноженной на (-3). Затем из первой строки вынесем общий множитель 3.