Основные действия над матрицами.
1. Сложение матриц.
Суммой двух матриц А и В одного и того же порядка называется матрица С того же порядка, все элементы которой равны сумме соответствующих элементов матриц А и В. Обозначают
А+В=С.
Если аij и 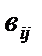 - элементы матриц А и В соответственно, то элемент матрицы С
- элементы матриц А и В соответственно, то элемент матрицы С 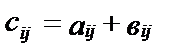 .
.
2. Умножение матрицы на число.
Произведением матрицы на число называется матрица, все элементы которой умножены на это число.
3. Транспонирование матрицы.
Если матрица А порядка т х п, то транспонированная матрица имеет порядок п х т и получается заменой строк столбцами. Обозначается Ат.
№ 11. Примеры.
Если 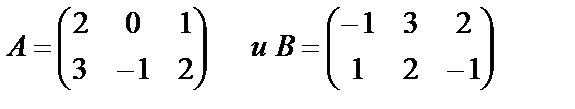 , то сумма С=А+В – матрица, равная
, то сумма С=А+В – матрица, равная 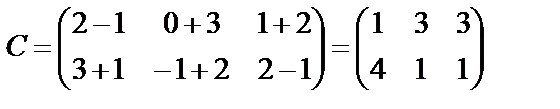 .
.
Произведение матрицы А на число k
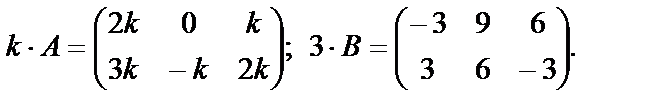
Найдем разность матриц
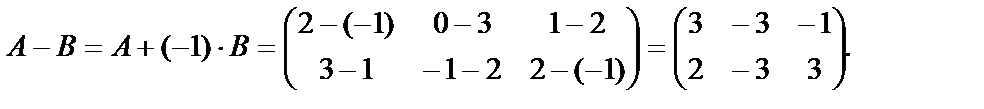
Транспонированные для матриц А и В матрицы
Ат= 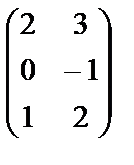 и Вт=
и Вт= 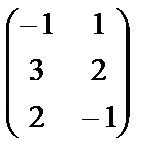 .
.
Заметим, что единичная матрица Е при транспонировании не меняется.
4. Умножение матрицы на матрицу.
Операция умножения матриц является исходным пунктом обширной теории – алгебры матриц, играющей важную роль в различных разделах математики и ее приложениях.
Пусть даны матрица А порядка т х р и матрица В порядка р х п. Обозначим
аik – элемент матрицы А, i=1,2,…,т; k=1,2,…,р;
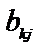 - элемент матрицы В, k=1,2,…,р; j=1,2,…,п.
- элемент матрицы В, k=1,2,…,р; j=1,2,…,п.
Произведением матрицы А на матрицу В называется матрица С порядка т х п, каждый элемент которой
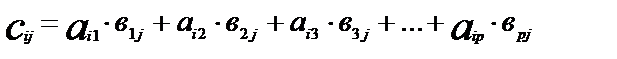 , т.е. элемент сij, стоящий в строке с номером i и столбце с номером j, равен сумме попарных произведений соответствующих элементов i-ой строки матрицы А и j-го столбца матрицы В.
, т.е. элемент сij, стоящий в строке с номером i и столбце с номером j, равен сумме попарных произведений соответствующих элементов i-ой строки матрицы А и j-го столбца матрицы В.
Из этого определения вытекает, что матрицу А можно умножать не на всякую матрицу В: необходимо, чтобы число столбцов матрицы А было равно числу строк матрицы В.
В качестве примера рассмотрим
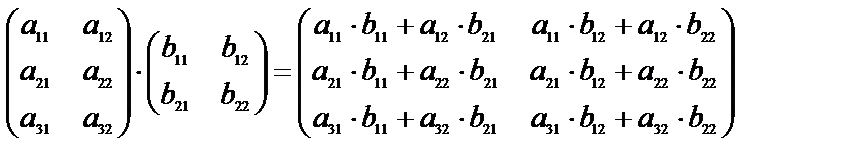 .
.
Записана формула умножения матрицы порядка 3х2 на матрицу порядка 2х2. Очевидно, если возможно умножение А×В, то умножение В×А не всегда возможно. Если обе матрицы квадратные одного порядка, то возможны умножения в любом порядке, но и тогда, как правило, 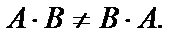
Например, если 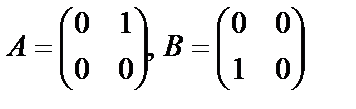 , то
, то 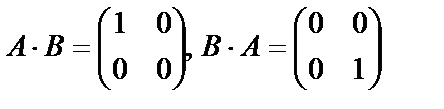 , т.е.
, т.е. 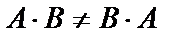 .
.
В случае, если одна из матриц – сомножителей является единичной, то А×Е=Е×А=А.
Заметим, что в этом случае А – квадратная матрица.
Пример.
№ 12. 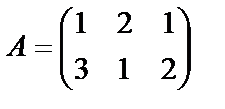 ,
, 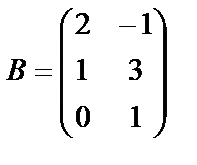 .
.
Найти произведения А×В и В×А.
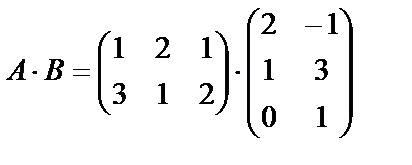 =
= 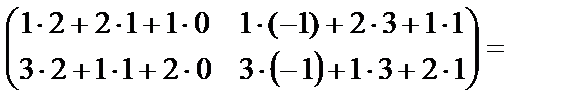
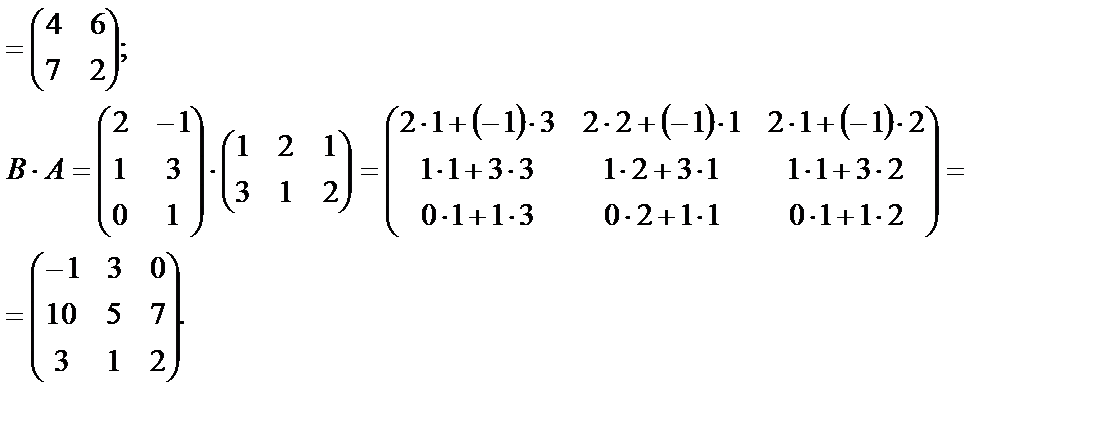
5. Обратная матрица
Действия над матрицами во многом аналогичны действиям над обычными числами. Среди чисел существует число 1 (единица) такое, что а×1=1×а=а для любого числа а.
Среди квадратных матриц роль такой «единицы» выполняет единичная матрица Е: А×Е=Е×А=А для любой квадратной матрицы А.
Для каждого числа а, отличного от нуля (а¹0), существует обратное число а-1 такое, что а×а-1=а-1×а=1.
Оказывается, что аналогичное свойство справедливо и для матриц, причем роль условия а¹0 играет условие
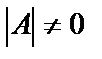 ,
,
где через |А| мы обозначаем определитель матрицы А. Матрица, определитель которой отличен от нуля, называется невырожденной, а матрица с определителем, равным нулю, называется вырожденной.
Матрица А-1 называется обратной по отношению к матрице А, если
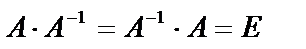 .
.
Итак, для всякой невырожденной матрицы существует обратная.
Правило отыскания обратной матрицы.
Пусть дана невырожденная квадратная матрица А порядка п и аij – элемент ее (i,j=1,2,…,п).
По условию определитель матрицы А 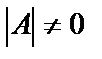 . Найдем для всех элементов аij матрицы их алгебраические дополнения Аij. Составим матрицу, заменив каждый элемент аij алгебраическим дополнением Аij. Естественно, это будет тоже квадратная матрица порядка п. Затем протранспонируем ее и умножим на число
. Найдем для всех элементов аij матрицы их алгебраические дополнения Аij. Составим матрицу, заменив каждый элемент аij алгебраическим дополнением Аij. Естественно, это будет тоже квадратная матрица порядка п. Затем протранспонируем ее и умножим на число 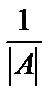 . Полученная матрица и будет обратной для матрицы А.
. Полученная матрица и будет обратной для матрицы А.
Итак, если
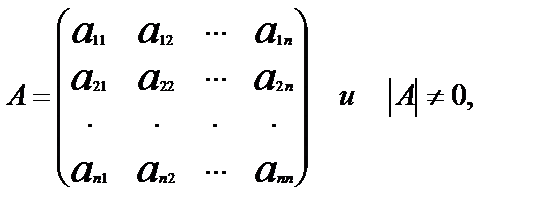 то обратная матрица
то обратная матрица
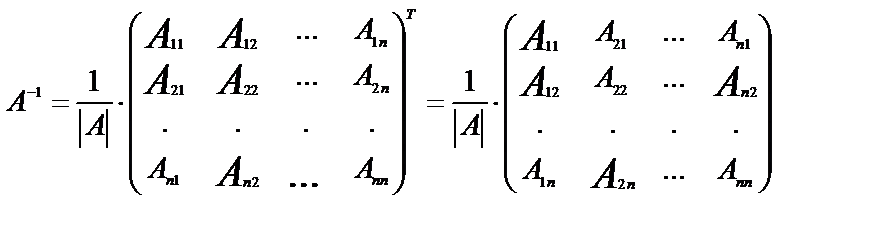 .
.
Для отыскания обратной матрицы необходимо:
1. Вычислить определитель 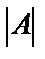 данной матрицы (должно быть
данной матрицы (должно быть 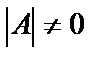 ).
).
2. Вычислить алгебраические дополнения Аij для всех элементов аij матрицы А по формуле Аij=(–1)i+j×Мij, где Мij – минор элемента аij.
3. Составить матрицу из алгебраических дополнений Аij.
4. Протранспонировать матрицу из алгебраических дополнений.
5. Полученную после транспонирования матрицу умножить на число 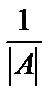 .
.
Пример.
№ 13. Найти обратную для матрицы 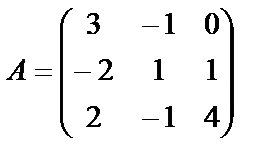
1) 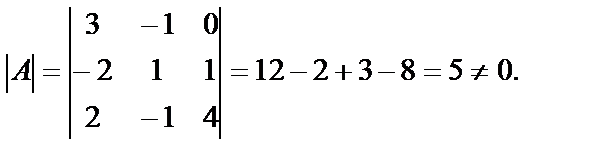
2) 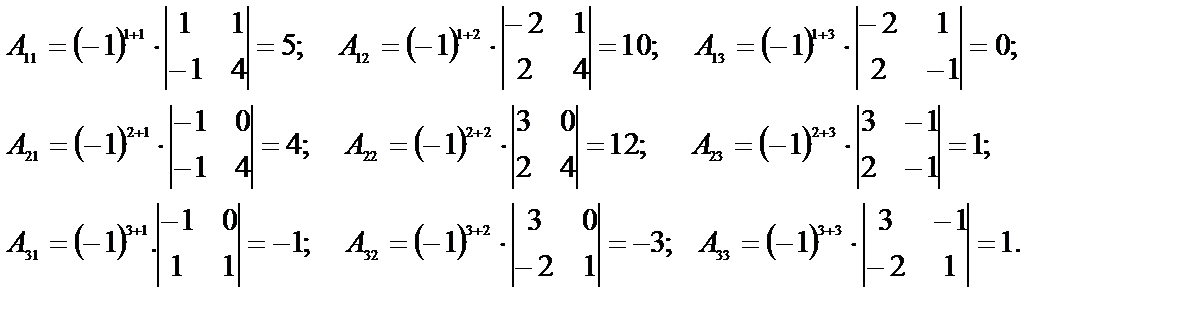
3) Составим матрицу из алгебраических дополнений
4) и протранспонируем ее:
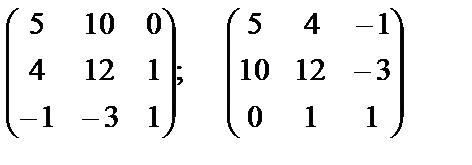 .
.
5) Умножив последнюю матрицу на число 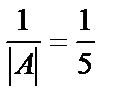 , получим обратную матрицу:
, получим обратную матрицу:
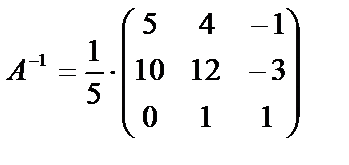
Убедимся в том, что обратная матрица найдена правильно:
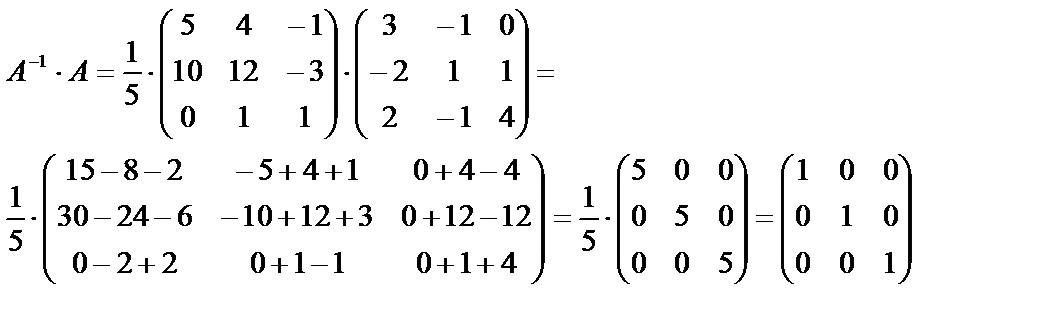
Так как 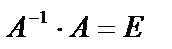 , то обратная матрица найдена верно.
, то обратная матрица найдена верно.
Дата добавления: 2014-12-30; просмотров: 1517;
