Метод Гаусса решения систем линейных уравнений

Мы рассматривали системы п линейных уравнений с п неизвестными. Рассмотрим произвольные системы линейных уравнений, в которых число уравнений т и число неизвестных п могут быть разными. Для таких систем решение не обязано быть единственным, если оно вообще существует. Возможны только три случая:

1) система не имеет ни одного решения (несовместна),

2) система имеет единственное решение,

3) система имеет бесчисленное множество решений.

Одним из наиболее удобных методов решения систем линейных уравнений является метод последовательных исключений неизвестных, или метод Гаусса.

Решим систему методом последовательного исключения неизвестных:

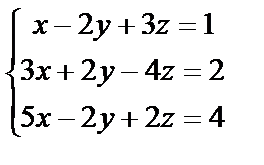(7)

Умножив первое уравнение на (-3), сложим со вторым, а умножив первое же уравнение на (-5), сложим с третьим. Получим систему, равносильную данной:

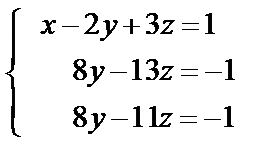(8)

Умножив второе уравнение системы (8) на (-1), сложим его с третьим:

Система 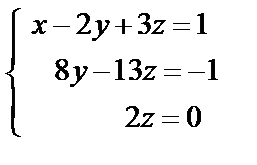(9)

равносильна данной, но решается очень просто снизу вверх: из третьего уравнения получим z=0, из второго у= – 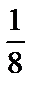, из первого .

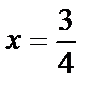Решение системы (7):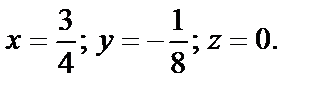

Сравним матрицы из коэффициентов при неизвестных систем (7), (8), (9).

.

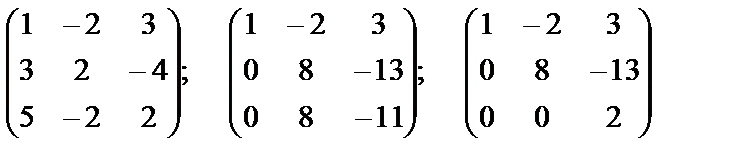Матрица системы (7) приведена к «треугольному» виду – матрице системы (9), определитель которой отличен от нуля как треугольный определитель. Значит, система имеет единственное решение, которое, кстати, очень просто теперь найти. Понятно, что удобнее проводить преобразования не с самими уравнениями системы, а только с матрицей из коэффициентов при неизвестных.

Перечислим так называемые элементарные преобразования матрицы:

1) умножение всех элементов на одно и то же число;

2) перестановка двух строк;

3) вычеркивание одной из двух пропорциональных или одинаковых строк;

4) вычеркивание строки, состоящей из одних нулей;

5) прибавление ко всем элементам какой-либо строки соответствующих элементов другой строки, умноженных на одно и то же число.

Матрица, полученная элементарными преобразованиями из данной матрицы, называется ей эквивалентный. Обозначается ~.

Запишем систему т линейных уравнений с п неизвестными:

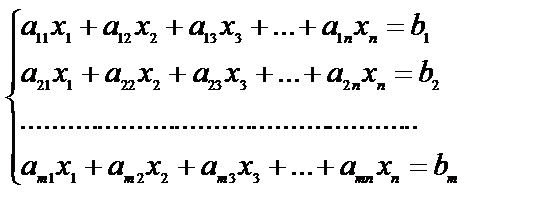
Матрица А порядка т х п, составленная из коэффициентов при неизвестных, называется основной матрицей системы.

Матрица В порядка т х (п+1), составленная из коэффициентов при неизвестных и столбца свободных членов, называется расширеннойматрицей системы. В ней столбец свободных членов принято отделять вертикальной чертой.

.

Для решения системы по методу Гаусса выписывают расширенную матрицу В системы и преобразовывают ее, чтобы получить в ней треугольник из нулей в нижнем левом ее углу.

Рассмотрим несколько примеров.

№ 15.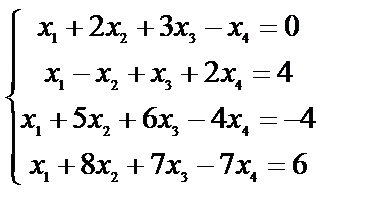

Выпишем расширенную матрицу В и при помощи первой ее строки получим нули в первом столбце.

~ ~

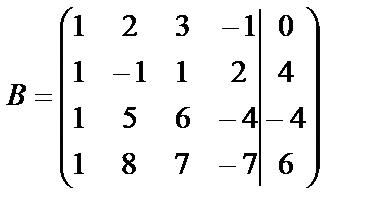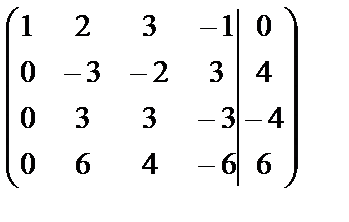Здесь мы вычли первую строку из каждой из последующих. Чтобы получить нули во втором столбце, используем вторую строку. Сложим ее с третьей; сложим ее и с четвертой, но предварительно умножим на 2.

В~ .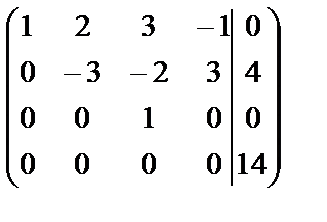

Полученная матрица свидетельствует о несовместности системы, т.к. последней ее строке соответствует уравнение 0×х₁+0×х₂+0×х₃+0×х₄=14, которое не может быть верным ни при каких х₁, х₂, х₃, х₄.

Итак, система несовместна (не имеет ни одного решения).

№ 16.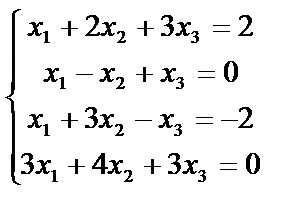

~ ~

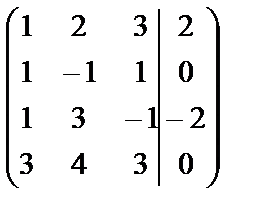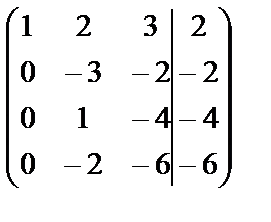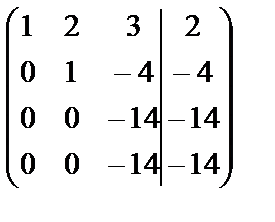
Мы переставили строки вторую и третью, чтобы иметь во втором столбце единицу и при помощи ее получить нули. В последней матрице две одинаковые строки, оставим одну из них. Окончательно имеем

.

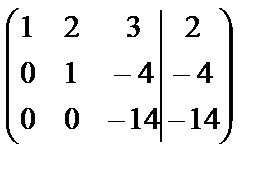Записав систему «снизу вверх», имеем

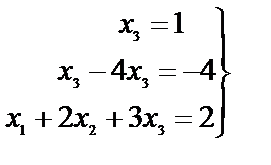
Система имеет единственное решение:

х₁= –1; х₂=0; х₃=1.

№ 17.

Преобразуем расширенную матрицу:

~ ~

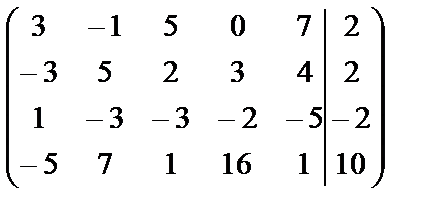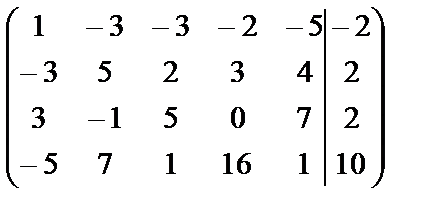Мы переставили местами первую и третью строки. Получим нули в 1^м столбце.

~

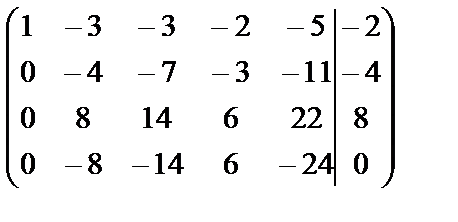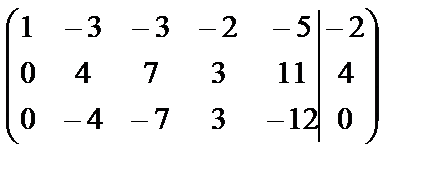
Последняя матрица получена после вычеркивания третьей строки (она пропорциональна второй) и деления на общие множители второй и последней строк. Сложив в последней матрице две последние строки, получим:

.

Из последней матрицы видно, что система не может иметь единственного решения, но она совместна. Значит, система имеет бесчисленное множество решений. Найдем их.

Так как полученная матрица содержит три строки, выделим столбцы, которые могут составить треугольный определитель, отличный от нуля. Например, первый, второй и пятый столбцы:

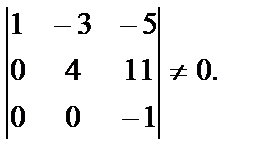
Эти столбцы соответствуют неизвестным х₁, х₂, х₅. Назовем их основными неизвестными. Остальные неизвестные назовем свободными неизвестными – это х₃ и х₄. Запишем систему «снизу вверх» так, чтобы свободные неизвестные были перенесены в правую часть соответствующего уравнения:

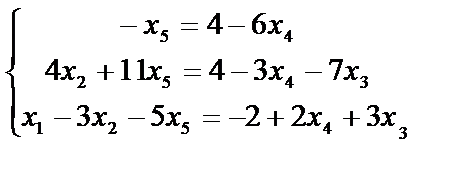
Определитель этой системы отличен от нуля, поэтому система может быть решена относительно основных неизвестных х₁, х₂, х₅ по формулам Крамера или непосредственно. Сначала х₅= –4+6х₄. Затем из второго уравнения х₂=12– 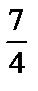х₃– 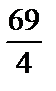х₄, а из первого уравнения х₁=14– 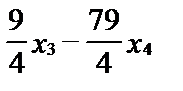, где х₃ и х₄ – свободные неизвестные, которые могут принимать любые значения. Например, при х₃=х₄=0, получим х₁=14, х₂=12, х₅= – 4.

Решением будут числа

х₁=14, х₂=12, х₃=0, х₄=0, х₅= –4.

Обычно свободные неизвестные обозначают буквами с, a, b и т.д.

Для нашей системы запишем ответ:

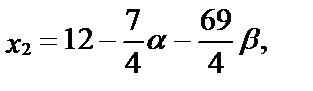
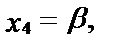
где a и b - любые числа.

Решая эту систему, мы выбрали в качестве основных неизвестных х₁, х₂, х₅. Можно было выбрать х₁, х₂, х₄, так как столбцы, им соответствующие, тоже составят определитель

Суммируя изложенное, подведем некоторые итоги, касающиеся метода Гаусса.

Метод Гаусса можно применить к любой системе линейных уравнений. Преобразуя расширенную матрицу системы, можем получить строку, содержащую слева от вертикальной черты только нули, а справа – отличное от нуля число. В этом случае система несовместна. Если такой строки в расширенной матрице мы не получим, то система совместна.

А именно: если слева от вертикальной черты получим матрицу с треугольным определителем, отличным от нуля, то система имеет единственное решение, которое легко получить, записывая уравнения «снизу вверх». Если слева от вертикальной черты основная матрица системы содержит в каждой строке более одного отличного от нуля элемента, то система имеет бесчисленное множество решений. В этом случае из всех неизвестных выбирают основные неизвестные – те неизвестные, коэффициенты при которых составят треугольный определитель, отличный от нуля. Оставшиеся неизвестные называют свободными. Полученную систему (она теперь крамеровская) решают, выражая основные неизвестные через свободные. Свободные неизвестные могут принимать любые постоянные значения.

Вопросы для самоконтроля

Прежде чем приступать к решению задач из контрольного задания, попробуйте ответить на предлагаемые вопросы. Если Вы затруднитесь с ответом, обратитесь вновь к теоретической части.

1) Чему равна сумма определителей

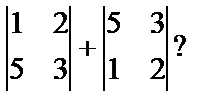
2) При помощи каких свойств удобнее вычислить определитель

3) Вычислить определители:

.

4) Найти числа а, в, с, d, если

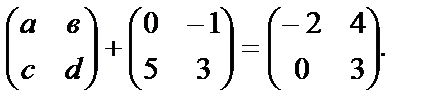
5) Возможно ли сложение матрицы–строки и матрицы–столбца?

6) Какая матрица получится в результате умножения произвольной матрицы на число 0?

Верно ли для любых двух матриц А и В равенство

0×А=0×В?

7) Для какой матрицы имеет смысл произведение

А×А=А²?

8) Пусть А - матрица порядка т х п. Какого порядка должна быть единичная матрица Е, чтобы имело смысл произведение

а) А×Е, б) Е×А?

9) При каком условии имеет смысл произведение произвольной матрицы порядка тхп

а) на матрицу – столбец?

б) на матрицу – строку?

Что представляет собой это произведение?

10) Найти матрицы А×В и В×А, есл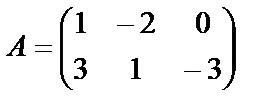и

и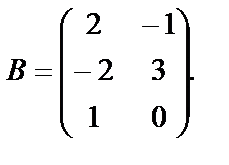

11) Какая матрица является транспонированной для матриц

Е×А и А×E?

12) Может ли быть несовместной однородная система линейных уравнений?

13) Каким условиям должны удовлетворять числа а₁, а₂, b₁, b₂, с₁, с₂, чтобы система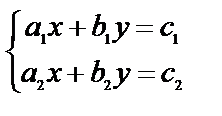

а) имела только нулевое решение?

б) была несовместной?

в) имела единственное решение?

г) имела бесчисленное множество решений?

1.8. Образец выполнения контрольного задания по теме «Элементы линейной алгебры»

Поскольку при заочном обучении у студентов возникают значительные трудности при решении задач, попытаемся дать подробное решение примеров, подобных тем, что включены в контрольное задание.

Задача №1.

Для вычисления определителя четвертого порядка используем свойства определителей, чтобы получить определитель третьего порядка.

.

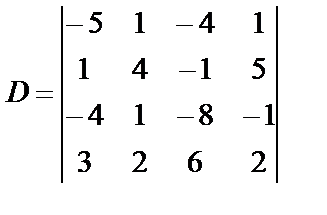Получим нули, например, во втором столбце, для чего элементы первой строки умножим на – 4 и прибавим к элементам второй. Те же элементы первой строки прибавим к третьей и четвертой строкам, но умноженные на–1 и на –2 соответственно.

После этого все элементы второго столбца, кроме первого элемента, будут нулями.

Мы использовали следствие из свойства 7. В определителе третьего порядка получим нули в последнем столбце (в нем один нуль уже есть). Мы не вычисляем определитель по правилу Сарруса, т.к. определитель содержит довольно большие числа. Итак, умножив на 2 первую строку, прибавим ее ко второй.

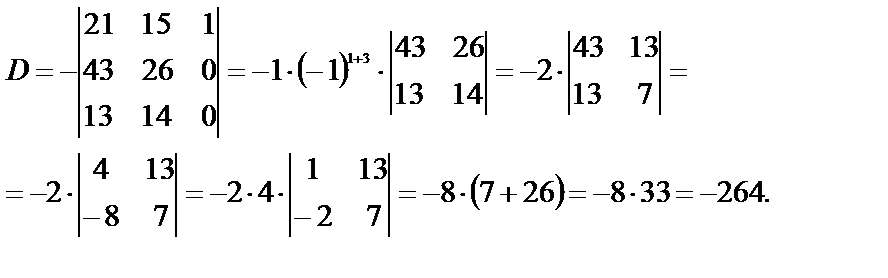
В определителе второго порядка вынесли общий множитель 2 из второго столбца. Далее можно получить в определителе числа, меньшие чем 43 и 13. Для этого второй столбец умножили на –3 и сложили с первым и вынесли общий множитель 4 из полученного первого столбца.

Можно вычислить определитель, приведя его к диагональному виду. Покажем и этот прием получения нулей под главной диагональю определителя. Для начала поменяем местами первую и вторую строки определителя (свойство 2).

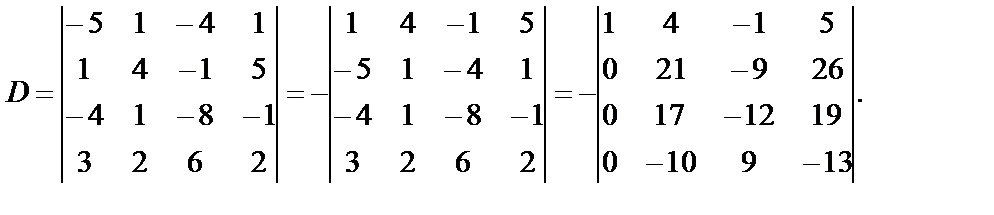
Для получения нулей во втором столбце удобно иметь числа, меньшие, чем 21, 17, –10. Умножив последнюю строку на 2, прибавим ее ко второй; к третьей строке прибавим четвертую.

Был получен диагональный определитель с элементами 1, 1, –11, –4 на главной диагонали. Учитывая множитель –6 перед определителем (общий множитель был вынесен из третьей строки – свойство 4), получим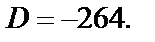

Задача №2.

Предлагается проверить законы линейной алгебры для матриц: сочетательные и распределительные законы сложения матриц и умножения матрицы на число.

Задача №3.

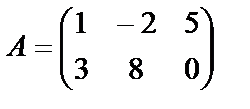и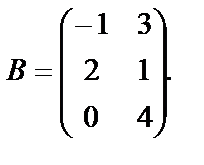

Найдем транспонированные матрицы:

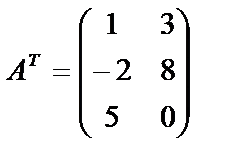и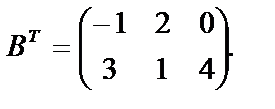

Найдем произведения матриц А×В и В^Т×А^Т.

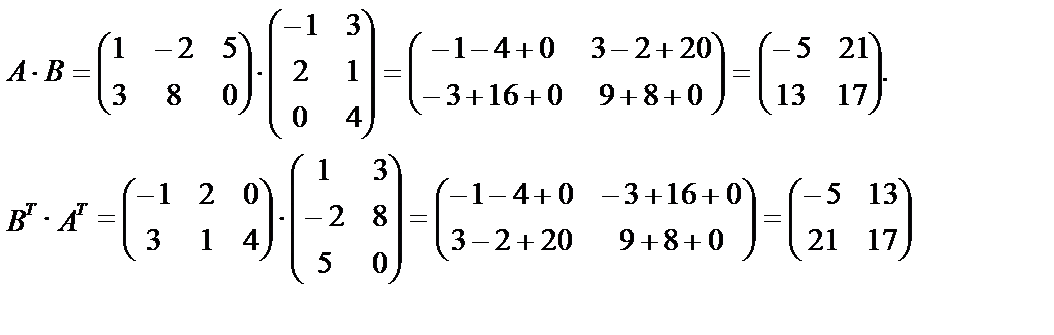
Действительно, .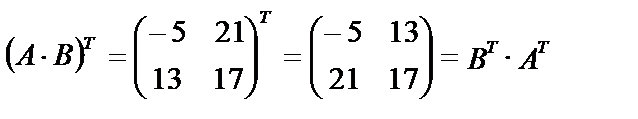

Задача №4.

Найти обратную матрицу для .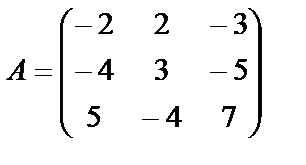

1. Вычислим определитель матрицы А по правилу Сарруса:

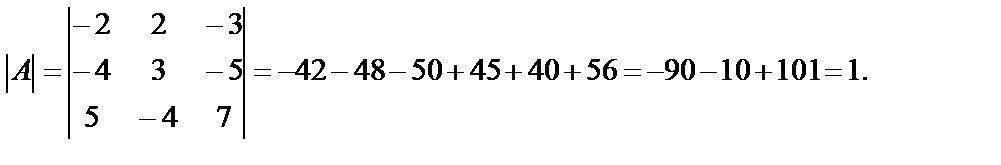
Т.к. |А|¹0, матрица А – невырожденная.

2. Вычислим алгебраические дополнения всех элементов матрицы А:

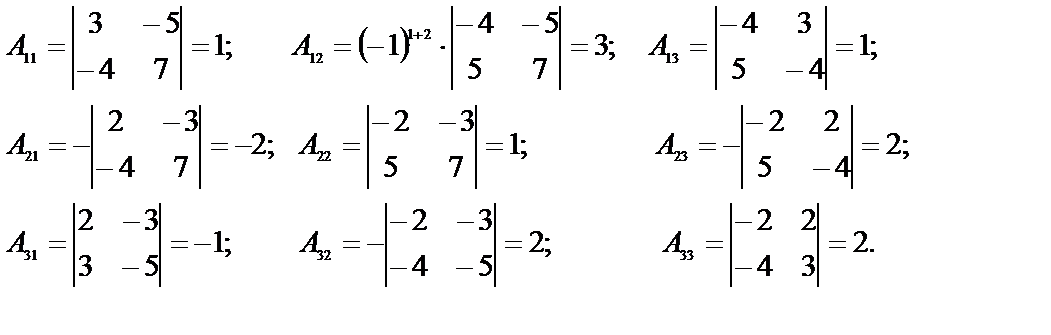
3. Составить матрицу из алгебраических дополнений .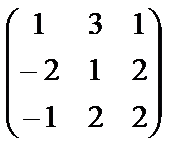

4. Протранспонируем эту матрицу

.

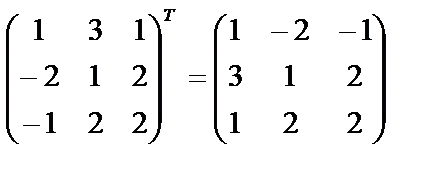5. Умножив последнюю матрицу на число 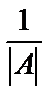, получим обратную матрицу:

.

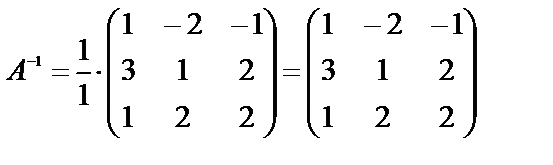6. Если матрица найдена верно, то А^-1×А=Е.

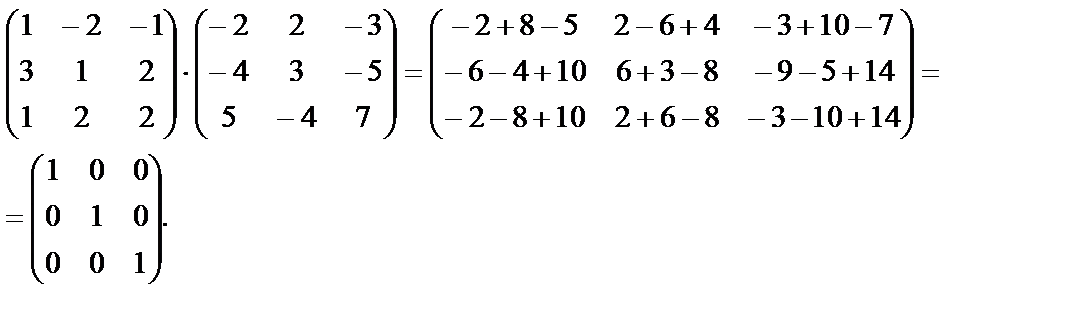
Обратная матрица найдена верно.

Задача №5.

Система линейных уравнений будет крамеровской, если ее определитель отличен от нуля (при числе уравнений равном числу неизвестных).

а) Решить по формулам Крамера систему

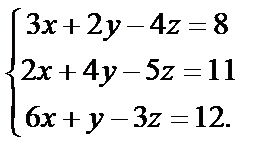
Вычислим определитель системы и определители при неизвестных:

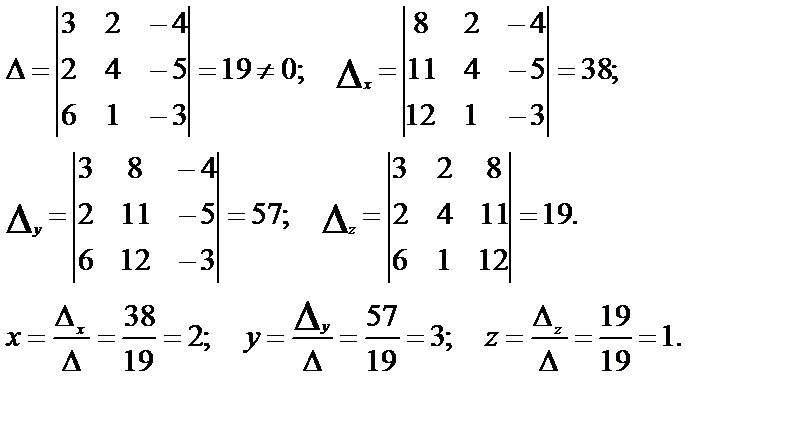
Подставим в каждое уравнение системы х=2, у=3 и z=1:

3×2+2×3–4×1=8 – верно,

2×2+4×3–5×1=11 – верно,

6×2+3–3×1=12 –верно.

Ответ: х=2, у=3, z=1.

б) Решить матричным способом систему

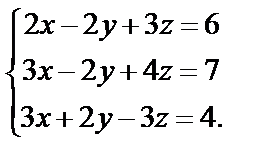
Запишем основную матрицу системы и вычислим ее определитель:

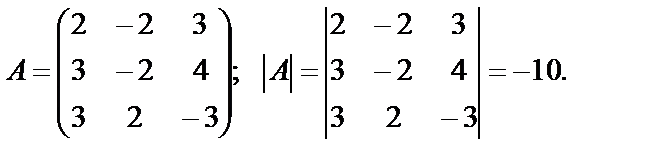
Т.к. |А|= –10¹0, то система крамеровская и для невырожденной матрицы А можно найти обратную.

А₁₁= –2; А₁₂=21; А₁₃=12;

А₂₁=0; А₂₂= –15; А₂₃= –10;

А₃₁= –2; А₃₂=1; А₃₃=2.

Обратная матрица А^-1:

Проверим, правильно ли найдена А^-1:

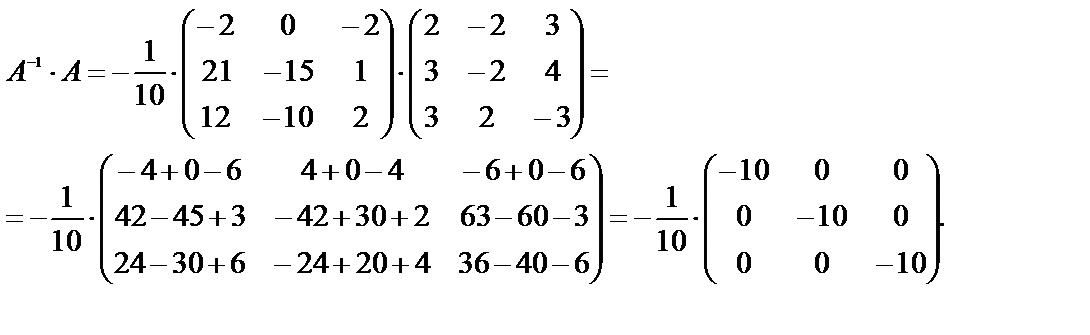
Действительно, 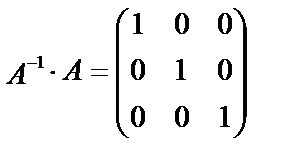, т.е. обратная матрица найдена правильно. Столбец из неизвестных получим из уравнения

Отсюда

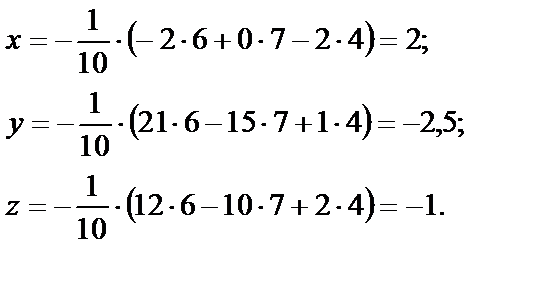
Подставим в каждое уравнение системы х=2, у= –2,5, z= –1.

2×2–2×(–2,5)+3×(–1)=6 – верно,

3×2–2×(–2,5)+4×(–1)=7 –верно,

3×2+2×(–2,5)–3×(–1)=4 – верно.

Ответ: х=2; у= –2,5; z= –1.

Задача №6.

Решить систему методом Гаусса:

1)

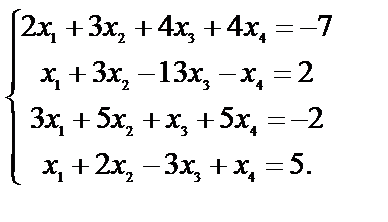
Выпишем расширенную матрицу В системы, предварительно поменяв местами первое и четвертое уравнения, чтобы иметь единицу в первой строке и первом столбце.

.

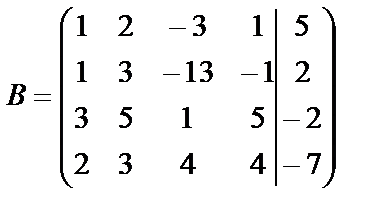Преобразуем матрицу В, чтобы получить в левом нижнем углу нули. В первом столбце нули получим при помощи первой строки, прибавляя ее ко второй, третьей и четвертой строкам, предварительно умножив ее на –1, –3, ‑2, соответственно. Получим матрицу, эквивалентную матрице В.

~ ~ .

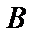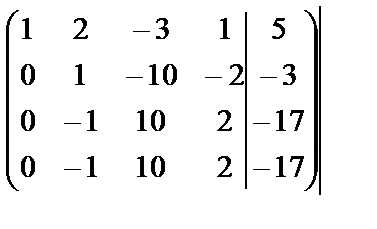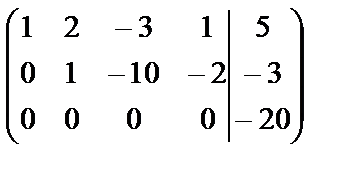Обнаружив две одинаковые строки, одну из них вычеркнем и прибавим к третьей строке вторую. В последней матрице третья строка говорит о несовместимости системы, т.к. не существует чисел х₁, х₂, х₃, х₄ таких, чтобы 0×х₁+0×х₂+0×х₃+0×х₄= –20.

Итак, система несовместна, т.е. не имеет решений.

2) Решим систему, относительно которой в примере №10 мы установили, что она крамеровская:

.

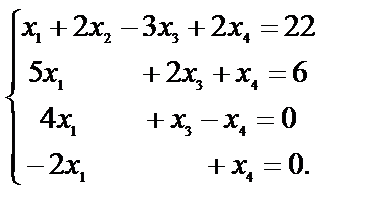
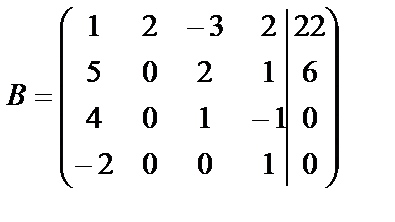Расширенная матрица В уже имеет во втором столбце три нуля, поэтому переместим столбцы, отметив, какой столбец какой именно неизвестной соответствует.

~ ~ ~

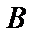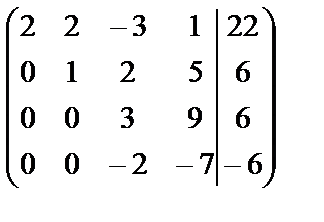х₂ х₄ х₃ х₁

~ ~

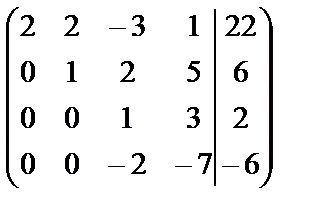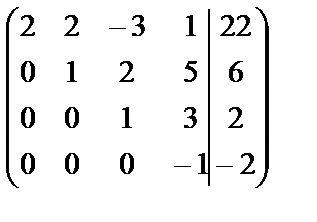
х₂ х₄ х₃ х₁

В последней матрице слева от черты получена матрица с треугольным определителем, отличным от нуля, что подтверждает, что система имеет единственное решение, которое мы получим «снизу вверх»:

–х₁= –2, х₁=2;

х₃+3х₁=2, х₃= –4;

х₄+2х₃+5х₁=6, х₄=4,

2х₂+2х₄–3х₃+х₁=22, х₂=0.

Ответ: х₁=2, х₂=0, х₃= –4, х₄=4.

3) Решим еще одну систему методом Гаусса:

.

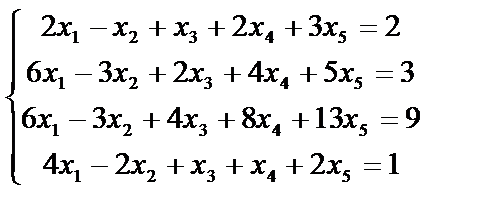Преобразуем расширенную матрицу к «треугольному» виду:

~ ~

~ ~ .

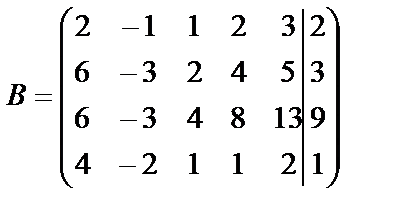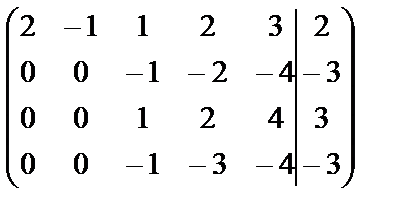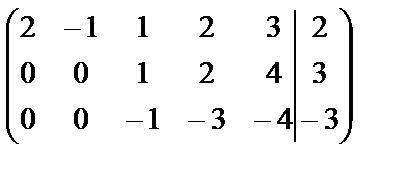Поясним наши действия. С помощью первой строки получили нули в первом столбце, одновременно получились нули и во втором столбце. С помощью второй строки получим нули в третьем столбце. Вычеркнем вторую строку в полученной матрице, т.к. она пропорциональна третьей строке, и сложим две последние строки. Из полученной последней строки сразу видно: х₄=0.

В последней матрице пунктиром выделим треугольный определитель, отличный от нуля. Неизвестные х₂, х₃, х₄, соответствующие этому определителю, назовем основными, а неизвестные х₁ и х₅ – свободными.

Запишем систему, соответствующую последней матрице, с неизвестными х₂, х₃, х₄, а слагаемые со свободными неизвестными х₁ и х₅ перенесем в правую часть каждого уравнения.

Эту систему легко решить «снизу вверх»:

х₄=0; х₃=3–4х₅; –х₂=2–2х₁–3х₅–3+4х₅; х₂=1+2х₁–х₅.

Обозначив х₁=a и х₅=b, получим ответ:

х₁=a; х₂=1+2a–b; х₃=3–4b; х₄=0; х₅=b, где a и b - любые числа.

Итак, рассмотренная система имеет бесчисленное множество решений, каждое из которых можно получить, выбирая произвольно постоянные a и b.