Матрицы. Действия над матрицами

Мы рассматривали системы, в которых число уравнений и число неизвестных одинаково. Перейдем теперь к системам более общего вида и запишем систему т линейных уравнений с п неизвестными:

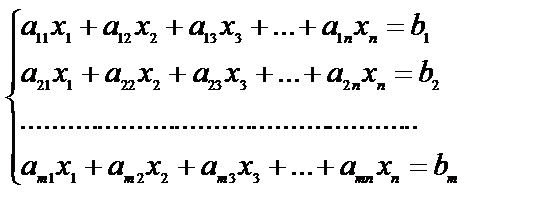
Таблицу из коэффициентов при неизвестных назовем прямоугольной матрицей порядка т х п и обозначим буквой А:

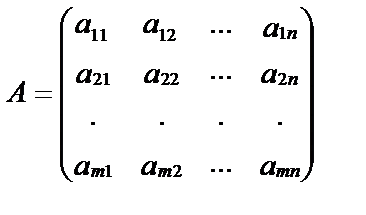
Матрица А состоит из т·п элементов, расположенных в т строках и п столбцах. Если а_ij – произвольный элемент матрицы, то индекс i (номер строки) принимает значения от 1 до т, индекс j (номер столбца) принимает значения от 1 до п. Записывают: i=1,2,3,…,т; j=1,2,3,..,п.

Например, 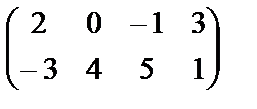- матрица порядка 2х4.

- матрица – строка порядка 1х5.

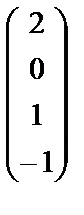- матрица – столбец порядка 4х1.

При т=п получим квадратную матрицу.

Квадратная матрица называется единичной, если ее главная диагональ состоит из единиц, а все другие ее элементы равны нулю. Единичная матрица обозначается буквой Е.

Так, 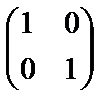- единичная матрица второго порядка.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается буквой О.

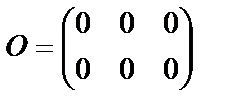- нулевая матрица порядка 2х3;

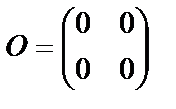- нулевая матрица порядка 2х2.