Системы линейных уравнений. Система m линейных уравнений с n неизвестными имеет следующий вид:

Система m линейных уравнений с n неизвестными имеет следующий вид:

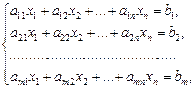(7)

где a_ij, b_i — произвольные числа ( 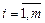; 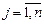), которые называются соответственно коэффициентами при неизвестных x_j и свободными членами уравнений (7).

Индекс i у коэффициентов при неизвестных означает номер уравнения, индекс j — номер неизвестного.

Решением системы (7) называется такой набор ( 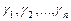) чисел 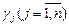, при подстановке которых вместо независимых x_j каждое уравнение системы превращается в тождество.

Система уравнений (7) называется совместной, если она имеет хотя бы одно решение. Если система не имеет решений, она называется несовместной.

Матрицу, составленную из коэффициентов при неизвестных, называют матрицей системы.

Рассматривают также расширенную матрицу, т. е. матрицу, полученную из матрицы системы присоединением к ней справа столбца свободных членов.

Теорема Кронекера-Капелли. Система (7) линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.