Типовая задача 4. Исследовать на совместность и решить систему уравнений

Исследовать на совместность и решить систему уравнений

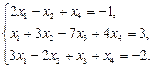
Решение. Находим ранги матрицы системы и расширенной матрицы:

.

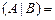
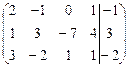
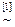
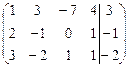
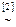
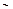
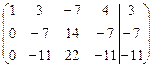
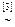
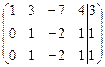
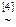
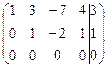[1]: Меняем местами первую и вторую строки.

[2]: Элементы первой строки умножим на (–2) и прибавим соответственно к элементам второй строки. Затем элементы первой строки умножим на (–3) и прибавим соответственно к элементам третьей строки.

[3]: Элементы первой строки разделим на (–7), а элементы второй строки — на (–11).

[4]: Из элементов второй строки вычтем элементы третьей строки.

Итак, .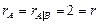

По теореме Кронекера-Капелли система совместна.

Так как 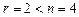, то система имеет бесконечное множество решений.

При помощи элементарных преобразований над уравнениями системы, аналогичных приведенным элементарным преобразованиям над строками матрицы, данная система приводится к виду

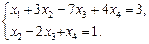
Перенеся члены со свободными неизвестными в правые части системы, получим: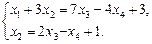

Давая свободным неизвестным х₃, х₄ произвольные значения t₁, t₂, получим общее решение системы: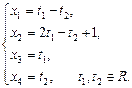

Ответ: .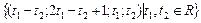

3. Задание 5
по теме «Теория пределов»

Краткие теоретические сведения