Элементарные функции
Основными элементарными функциями называют следующие функции:
Постоянную функцию у = с, с — const.
Степенную функцию у = х 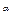 ,
, 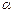 — любое действительное число.
— любое действительное число.
Показательную функцию у = ах (0 < a 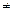 1).
1).
Логарифмическую функцию 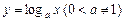 .
.
Тригонометрические функции y = sin x, y = cos x, y = tg x,
y = ctg x.
Обратные тригонометрические функции y = arcsin x, y = arccos x,
y = arctg x, y = arcctg x.
Функцию, аналитическое выражение которой можно получить при помощи конечного числа арифметических операций над основными элементарными функциями, а также при помощи операции взятия функции от функции, назовем элементарной функцией.
Пример.
Функции f(x) = arcsin(log5(x2 + 1)), f(x) = 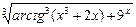 , f(x) =
, f(x) = 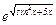 являются элементарными.
являются элементарными.
Областью определения D(y) функции y = f(x) называется множество значений аргумента х, для каждого из которых существует вполне определенное числовое значение функции.
Теорема. Если 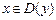 элементарной функции y = f(x), то
элементарной функции y = f(x), то 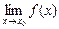 = f(x0).
= f(x0).
Например, 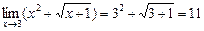 .
.
Дата добавления: 2014-12-02; просмотров: 1253;
