Типовая задача 6
Найти производные следующих функций:
у = (ln2 x + 5x)10;
у = (5cos3x + x) · tg3x;
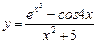 .
.
Решение. Используя формулы и правила дифференцирования, находим производные данной функции следующим образом:
1) 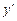 = ((ln2 x + 5x)10)' = 10 · (ln2 x + 5x)9 · (ln2 x + 5x)' = 10 · (ln2 x +
= ((ln2 x + 5x)10)' = 10 · (ln2 x + 5x)9 · (ln2 x + 5x)' = 10 · (ln2 x +
+ 5x)9 · 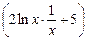 = 10 · (ln2x + 5x)9 ·
= 10 · (ln2x + 5x)9 · 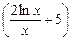 .
.
2) 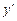 =((5cos3x + x) · tg3x)' = (5cos3x + x)' · tg3x + (5cos3x + x) · (tg3x)' =
=((5cos3x + x) · tg3x)' = (5cos3x + x)' · tg3x + (5cos3x + x) · (tg3x)' =
= (5cos3x · ln5 · (cos3x)' + 1) · tg3x + (5cos3x + x) · 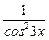 · 3 = (–5cos3x · ln5 · · sin3x · 3 + 1) · tg3x + (5cos3x + x) ·
· 3 = (–5cos3x · ln5 · · sin3x · 3 + 1) · tg3x + (5cos3x + x) · 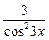 = (–3 · ln5 · 5cos3x · sin3x +
= (–3 · ln5 · 5cos3x · sin3x +
+ 1) · tg3x + 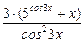 .
.
3) 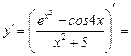 =
= 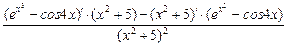 =
=
= 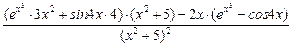 =
=
= 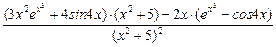 .
.
Ответ: 1) 10 · (ln2 x + 5x)9 · 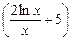 ;
;
2) (–3 · ln5 · 5cos3x · sin3x + 1) · tg3x + 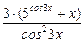 ;
;
3) 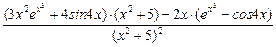 .
.
Дата добавления: 2014-12-02; просмотров: 826;
